剛体モデルによる筋張力の推定 例２

股関節外転運動時に中殿筋が発揮する張力の大きさは？

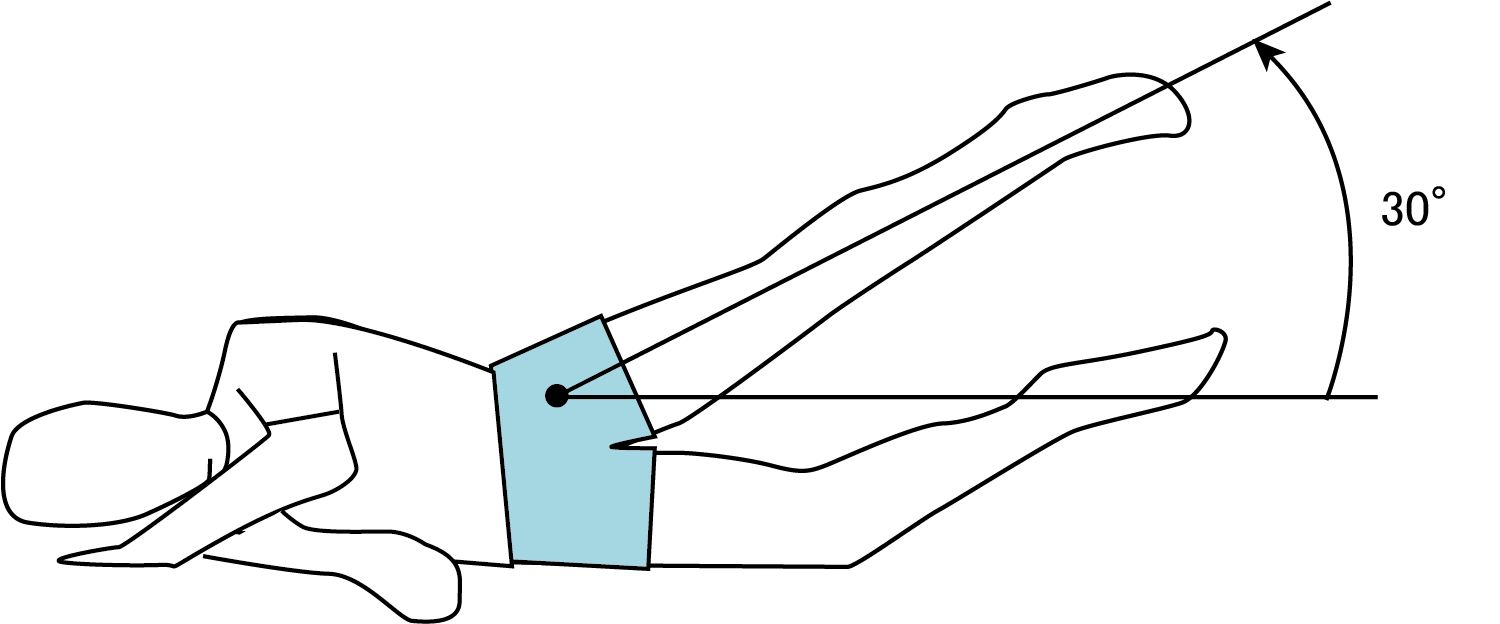
この例では側臥位で左股関節を外転３０度で保持しているところを想像します。この運動でも筋力強化のため、足関節周囲に重錘バンドを巻きつけることもあります。今回も例１と同様、重りなしの条件で見ていきます。この時に強く収縮するのはのの外転筋である中殿筋です。
では、この時、どこを剛体とすればよいでしょうか？ ここで着目しているのは股関節の回転運動です。足と下腿と大腿の下肢をひとつの剛体とするという仮定が適切です。

この「下肢」は股関節だけで回転します。肘関節が回転の中心となる「軸」です。

中殿筋の走行を考慮して作用線を描きます。中殿筋は腸骨稜と大転子の間にある筋です。

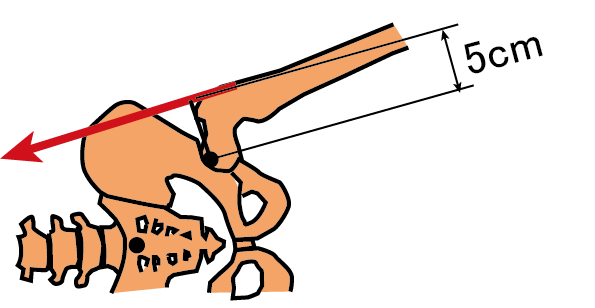
股関節運動の剛体モデルを単純化して、計測してわかる、あるいは、推定してわかる値を書き加えてみます。

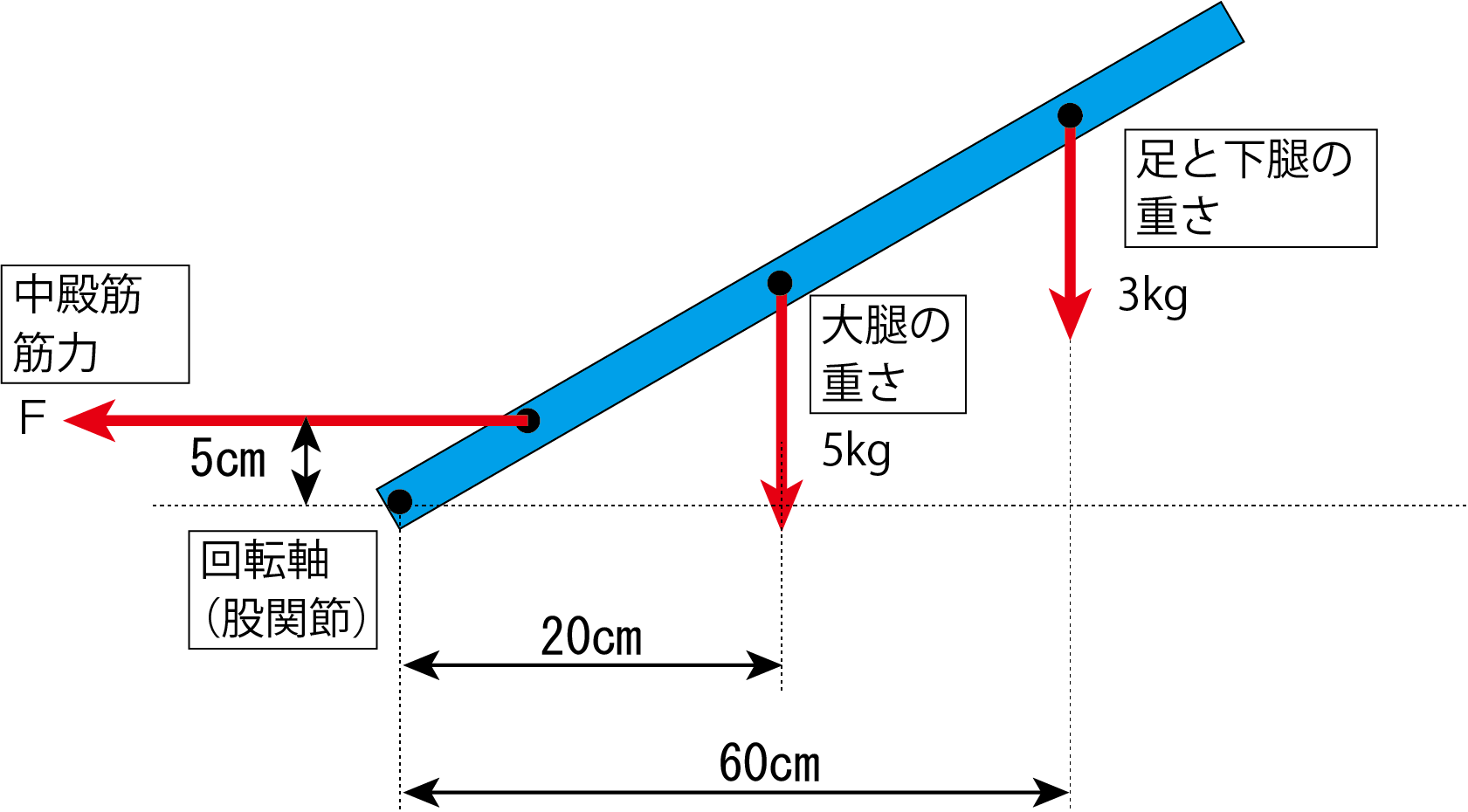
今回、下肢全体の重心と質量はわからないが、「大腿」と「下腿と足部」の重心と質量はわかっているとします。先に下肢の合成重心を求めてもよいのですが、「モーメントのつり合いの式」を立てて、中殿筋の力を求めてみます。

股関節を回転の中心とし、時計回りの回転方向をプラスとします。
-5 cm × F + 20 cm × 5 kg + 60 cm × 3 kg ＝ 0
これを解いて、
F＝56 kg

今回、中殿筋の張力Fは56kg（約560N）と推測されました。

分力に分ける vs. モーメントアームを求める

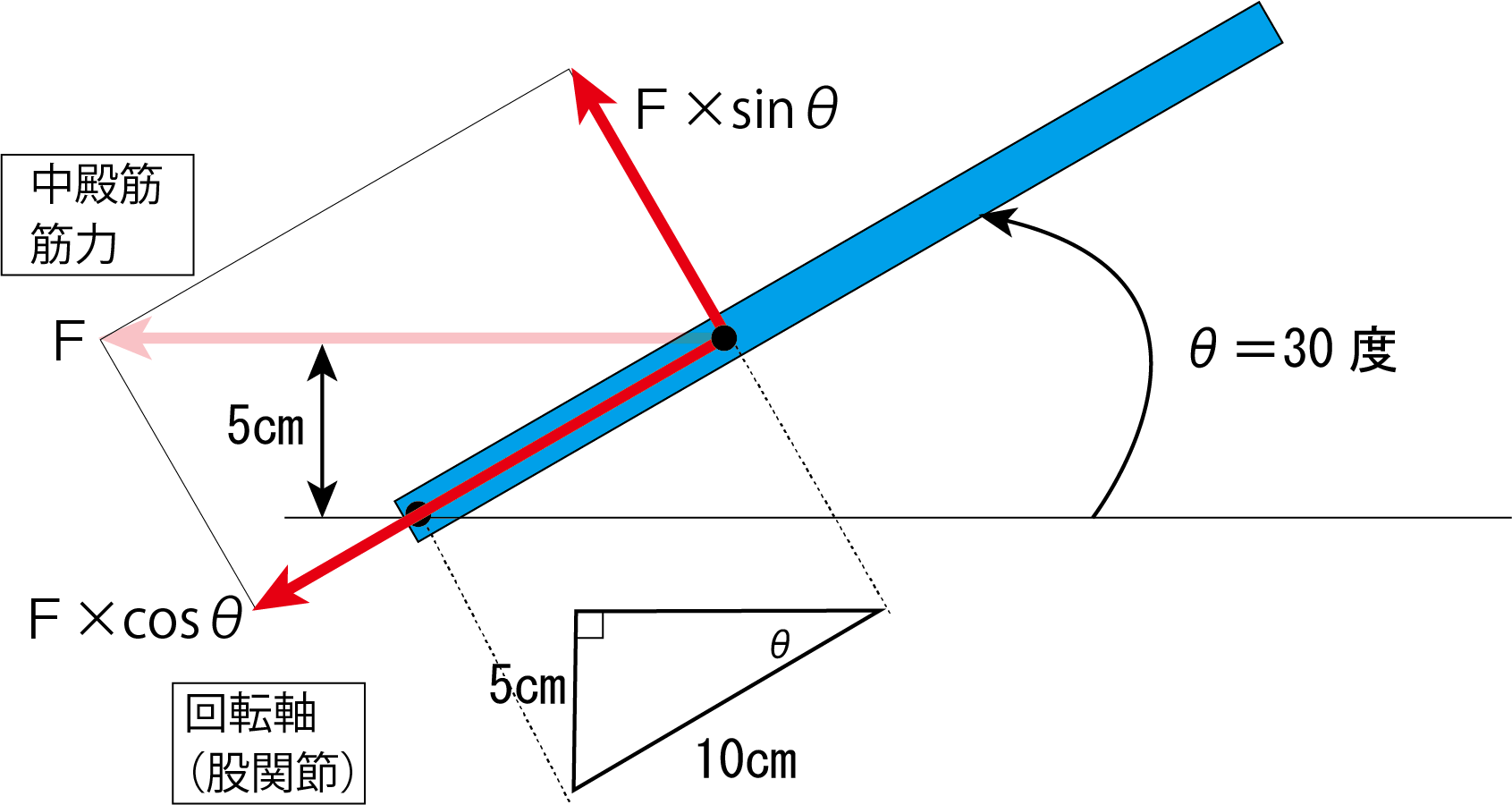
今回は股関節の軸から中殿筋の筋力の作用方向までの直線距離である、モーメントアームが５cmであるということがわかっており、これを使って筋力を計算しました。例１では、筋の付着位置までの距離が求められ、力を分力に分けて計算しましたが、この２つのやり方、どちらをとってもよいです。例えば、今回、モーメントアームは５cmでしたが、これを元に、股関節軸と筋の付着位置までの距離を計算すると
5 cm × (1/sinθ)＝10cmです。
この距離と垂直の力はF × (sinθ)です。両者をかけ合わせると、F × (sinθ)×10cmと(sinθ)はθが３０度の時、1/2なので
F × 5cmとなり、モーメントアームをかけ合わせたときと同じになります。

先頭に戻る