剛体モデルによる筋張力の推定

リンゴを持った時、上腕二頭筋が発揮する張力の大きさは？

リンゴを手のひらにのせて持ったところを想像して下さい。どこに力が入るでしょうか？筋肉は収縮すると硬くなるので、腕のどの部分が硬くなったか触ってみてください。前腕の前面や上腕の前面に何か感じませんか？重力によって肘や手が伸展しないよう、手の屈筋や肘の屈筋が働き支えているはずです。
ここでは、肘の屈筋にどのくらいの張力が働いているかを考えてみます。手の屈筋も働いているでしょうが、手と肘、一度に二つの力を考えるのは難しいので、肘だけに的を絞ります。そこで、モデルでは、手と前腕が合体して一つになったモデルを考えます。 これを手と前腕をひとつの剛体とするという考えです。

この「前腕と手」は肘関節だけで回転できます。肘関節を「支点」と考えてもよいし、回転の中心となる「軸」と考えてもよいし、いずれにしても、この剛体は支点、あるいは軸のまわりで回転できます。もし、何の力も作用しなければ、この剛体はこの位置を保っていられません。重力の作用で時計回りに回転してしまうはずです。

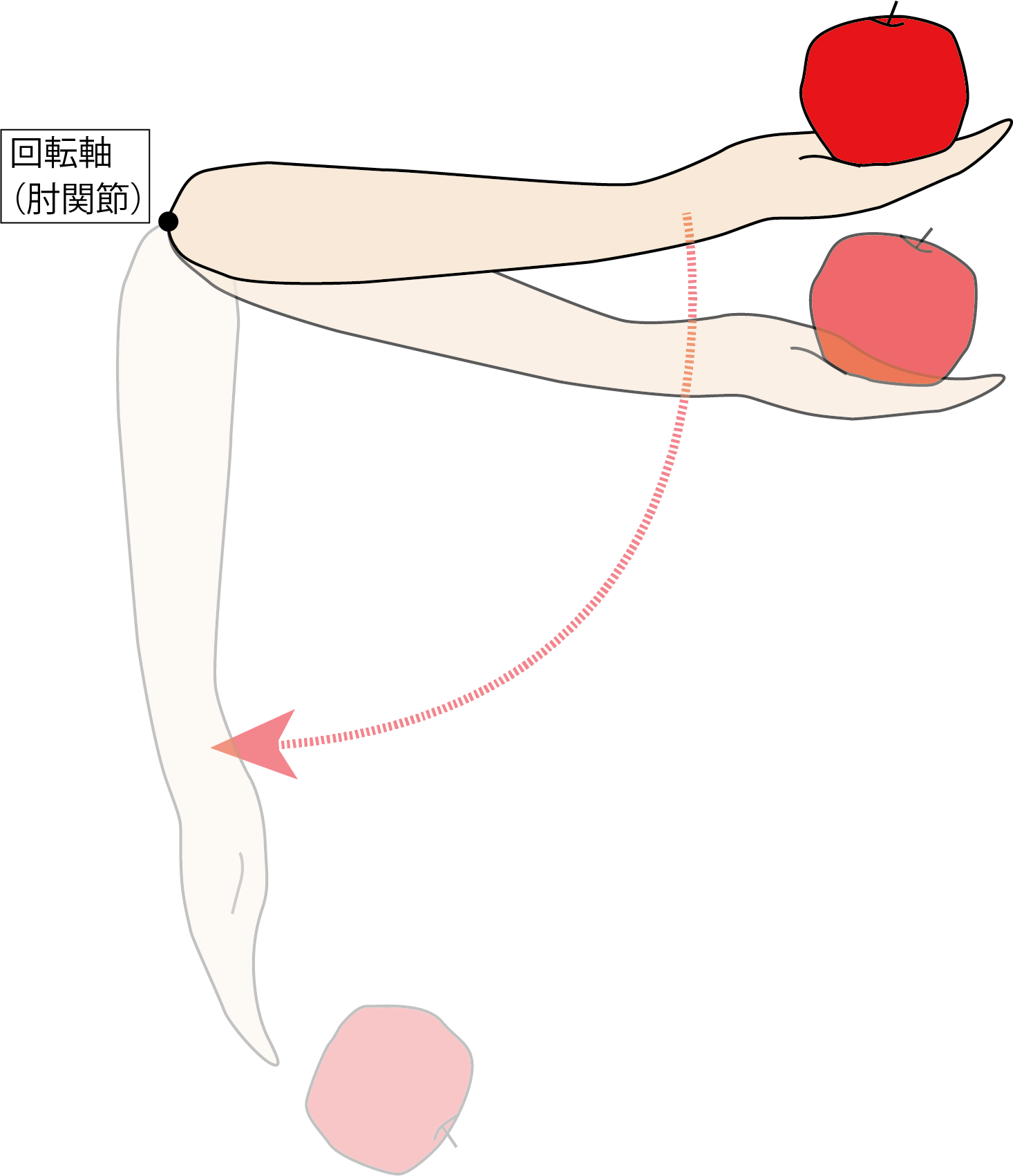
回転せず止まっていられる、肘を９０度に屈曲して保持できるのは、肘関節の屈筋が収縮して成り立ちます。肘の屈曲作用を持つ筋はいくつかありますが、ここでは、上腕二頭筋のみが働くと仮定します。
上腕二頭筋は烏口突起と関節上結節が起始で、橈骨粗面に停止します。この走行を考慮して上腕二頭筋の作用線を描きます。また、手と前腕の重心には、その重さによる力が、また、手のひらにも、のせているリンゴの重さによる力がかかります。これらを合わせて描くと次のようになります。

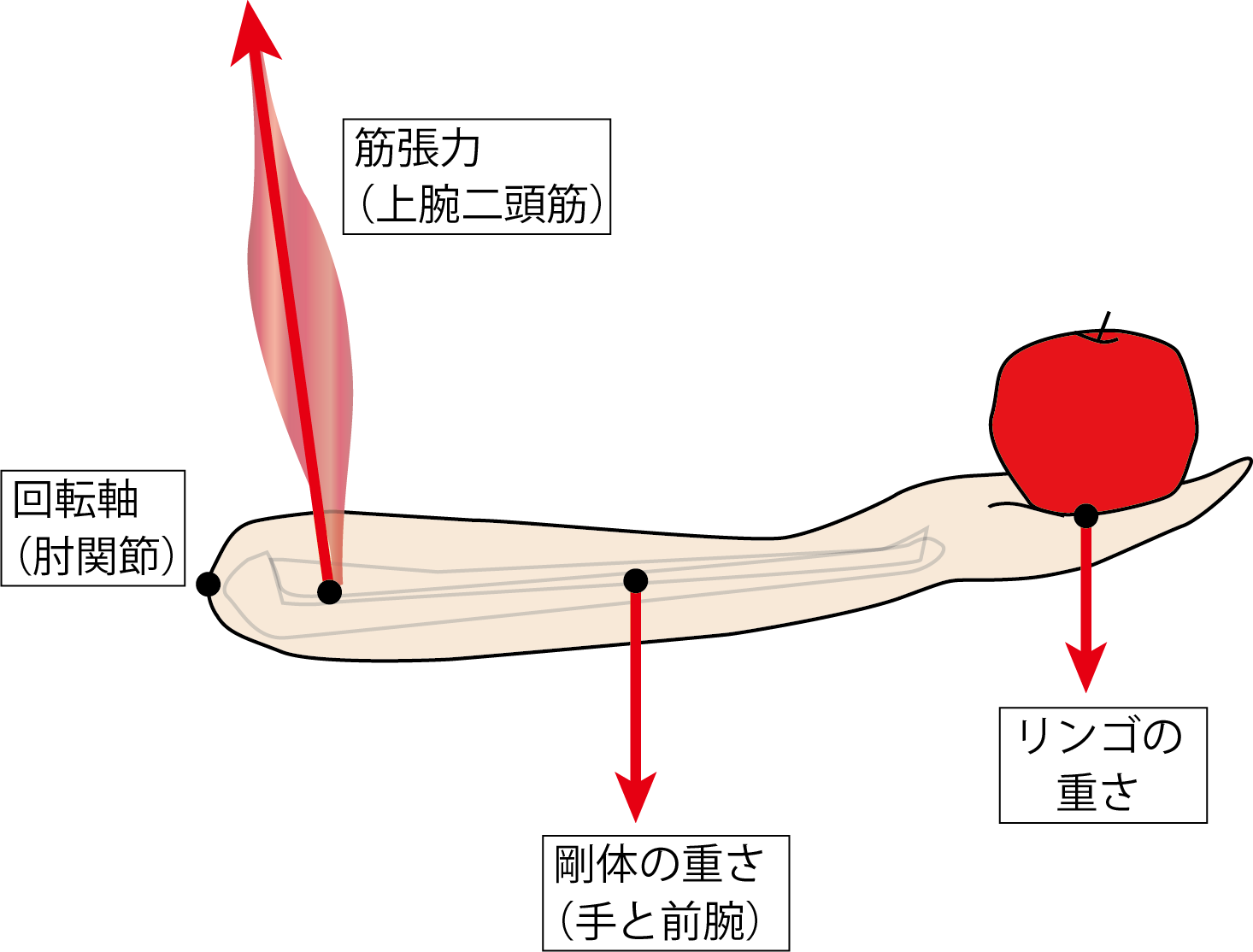
この図をもっと単純化して、計測してわかる、あるいは、推定してわかる値を書き加えてみます。
すると、どうしてもわからないのは、上腕二頭筋の力だけだと気づきます。

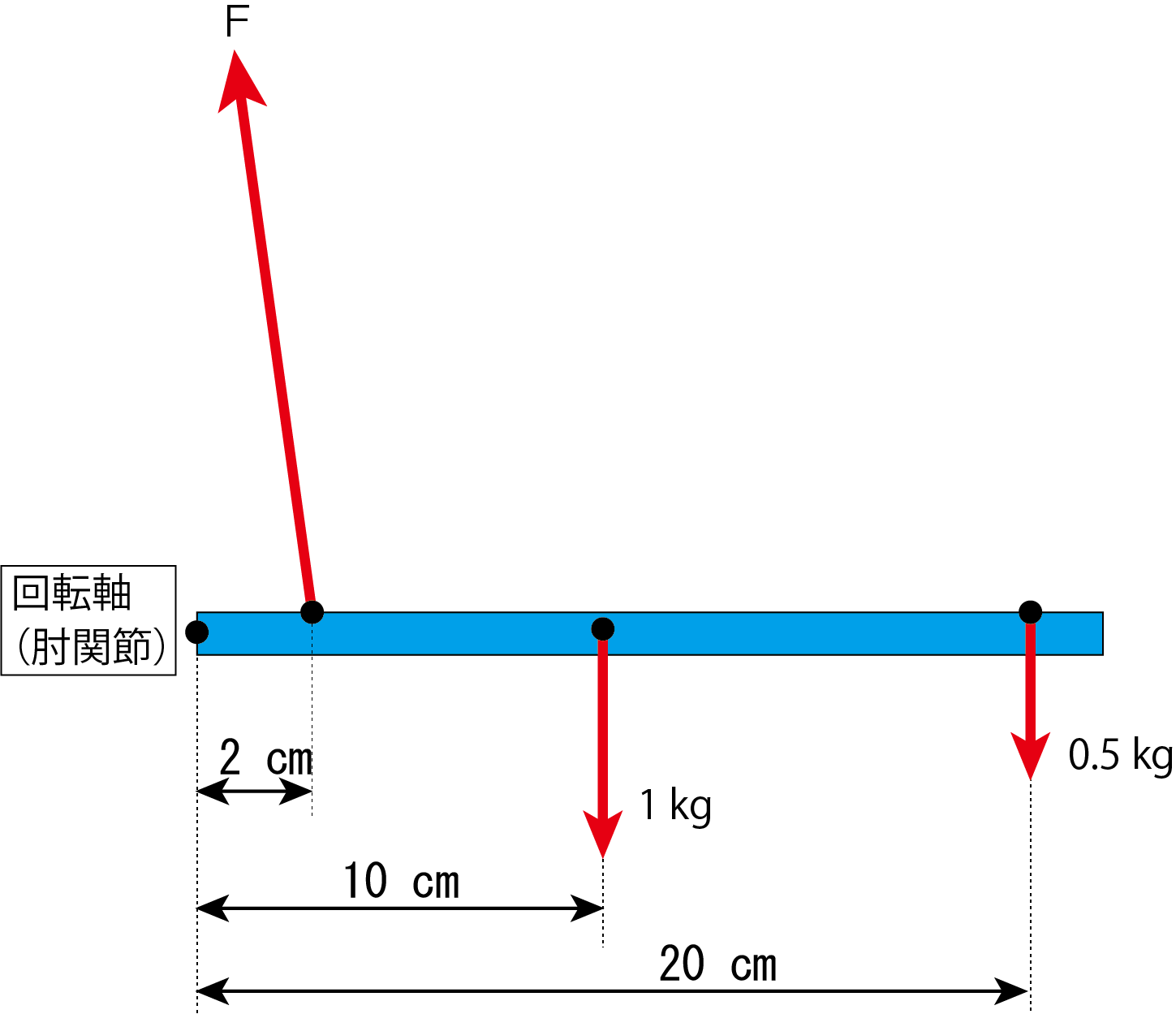
数値が入りましたので、「モーメントのつり合いの式」を立てることで、不明だった上腕二頭筋の力を求めることができます。ただし、この絵のように、力の方向が与えられている「回転軸から筋の付着までの距離」に対して垂直ではありません。モーメントの力×距離の「距離」は回転中心と力までの垂直方向距離です。そのため、一度力Fを垂直方向と水平方向に分けます。

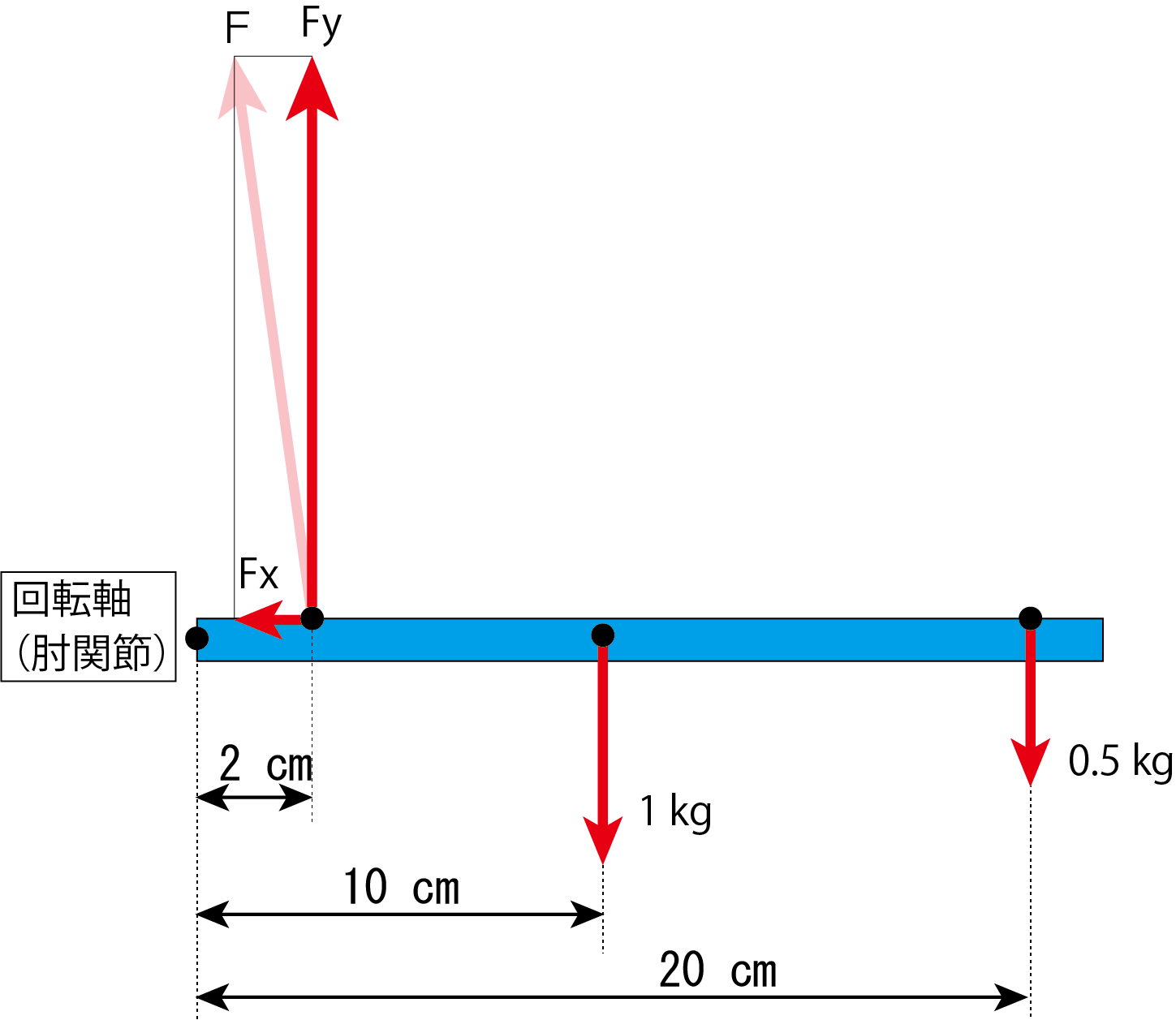
この図では水平方向をX軸、垂直方向をY軸として、上腕二頭筋の筋張力Fの水平方向分力をFx、垂直方向分力をFyとしています。これで、「モーメントのつり合いの式」を立てる準備が整いました。実際に計算式を立てて上腕二頭筋の張力を割り出してみます。

肘関節を回転の中心とし、時計回りの回転方向をプラスとします。
-０ cm × Fx - 2 cm × Fy + 10 cm × 1 kg + 20 cm × 0.5 kg ＝ 0
これを解いて、
Fy＝10 kg

さて、ここで本当に知りたいのは、分力Fyではなく、Fです。今、上腕二頭筋の力の方向がX方向から８０度傾斜しているとします。三角関数を使うと、FとFyの関係は次のように表せます。
Fy＝F × sin (80度)
三角関数表からsin (80度)は約0.98です。F＝Fy ÷ sin (80度)、F＝10 kg ÷ 0.98からF＝10.2 となります。今回は上腕二頭筋の作用方向がほぼ垂直だったので、FもFyもあまり大きな差はありません。ただ、関節の角度によっては変わってきますので、筋の力の方向をしっかりと意識しておくことが大切です。 いくつかの例で見ていきます。

例１：膝関節の伸展筋張力の推定

例２：股関節外転筋張力の推定

例３：足底屈筋の張力の推定

「剛体モデルによる筋張力の推定」のまとめ

• 関心のある関節を中心に、どこが剛体か、を適切に見立てる。
• 剛体に作用する力を全て上げ、わかっている距離や力を書き加える
• モーメントのつり合い式を立てて筋張力を導く

先頭に戻る