剛体モデルによる筋張力の推定 例１

膝伸展運動時に大腿四頭筋が発揮する張力の大きさは？

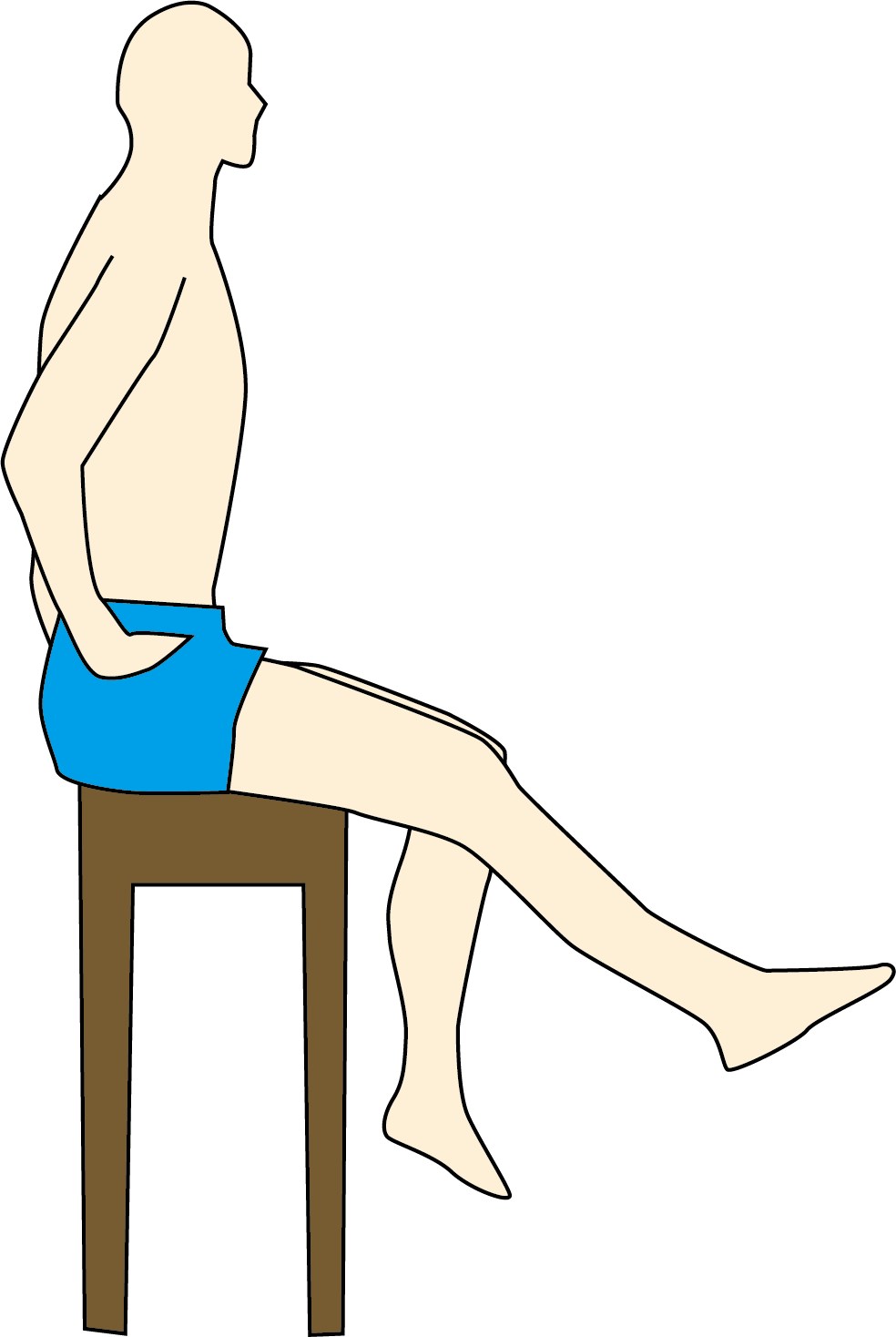
この例では椅子に座って右膝関節を伸ばしているところを想像します。筋力強化のため、足関節周囲に重錘バンドを巻きつけることもありますが、今回は重りなしの条件で見ていきます。膝を完全に伸展して保持した際、強く収縮するのは大腿四頭筋です。
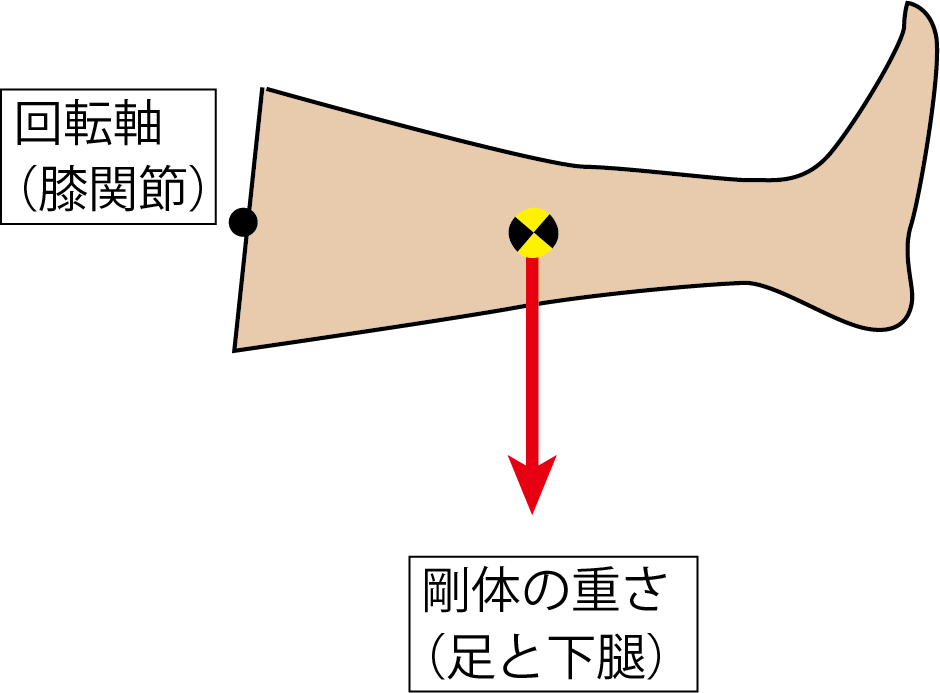
ここでは、座位で膝関節を伸展して保持しているときの大腿四頭筋の張力を考えてみます。では、この時、どこを剛体とすればよいでしょうか？下肢全体？大腿？下腿？足部？どこでしょうか？ リンゴを持つ手と同じように、ここで着目しているのは膝関節の回転運動ですので、足と下腿をひとつの剛体とするという仮定が適切です。

この「下腿と足部」は膝関節だけで回転します。肘関節が回転の中心となる「軸」です。

大腿四頭筋の起始は４つの筋で様々ですが、最終的には膝蓋骨を経由し脛骨粗面に停止します。この走行を考慮して大腿四頭筋の作用線を描きます。膝蓋骨が滑車のような役割をするので、下腿の長軸方向に対して３０度くらい傾斜しています。

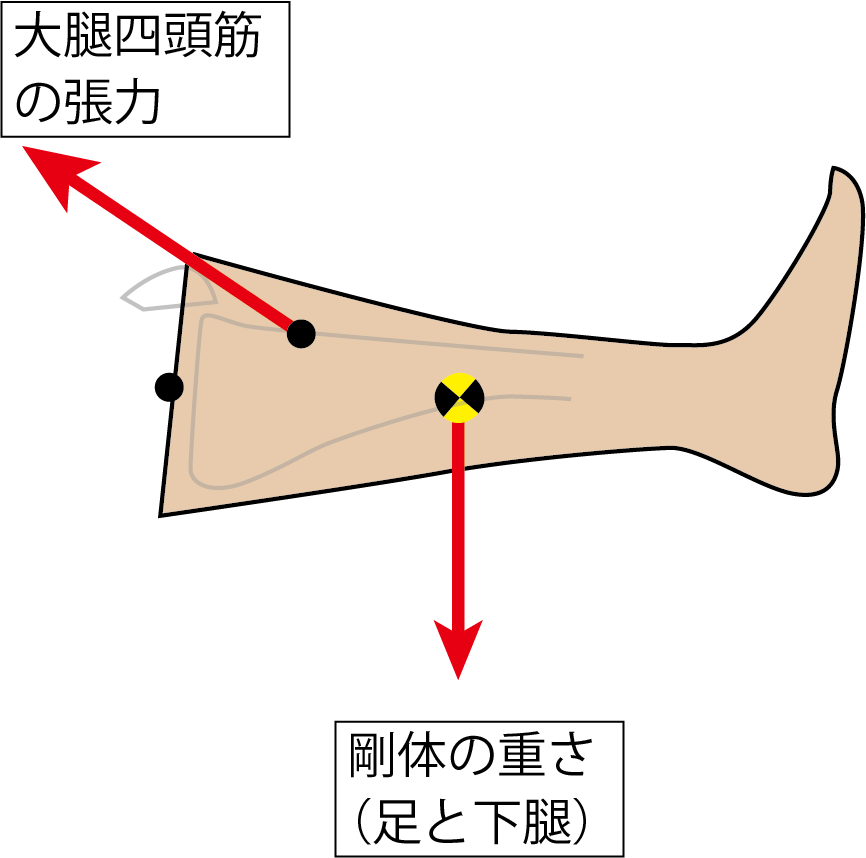
この図をもっと単純化して、計測してわかる、あるいは、推定してわかる値を書き加えてみます。
わからないのは、大腿四頭筋の力だけです。

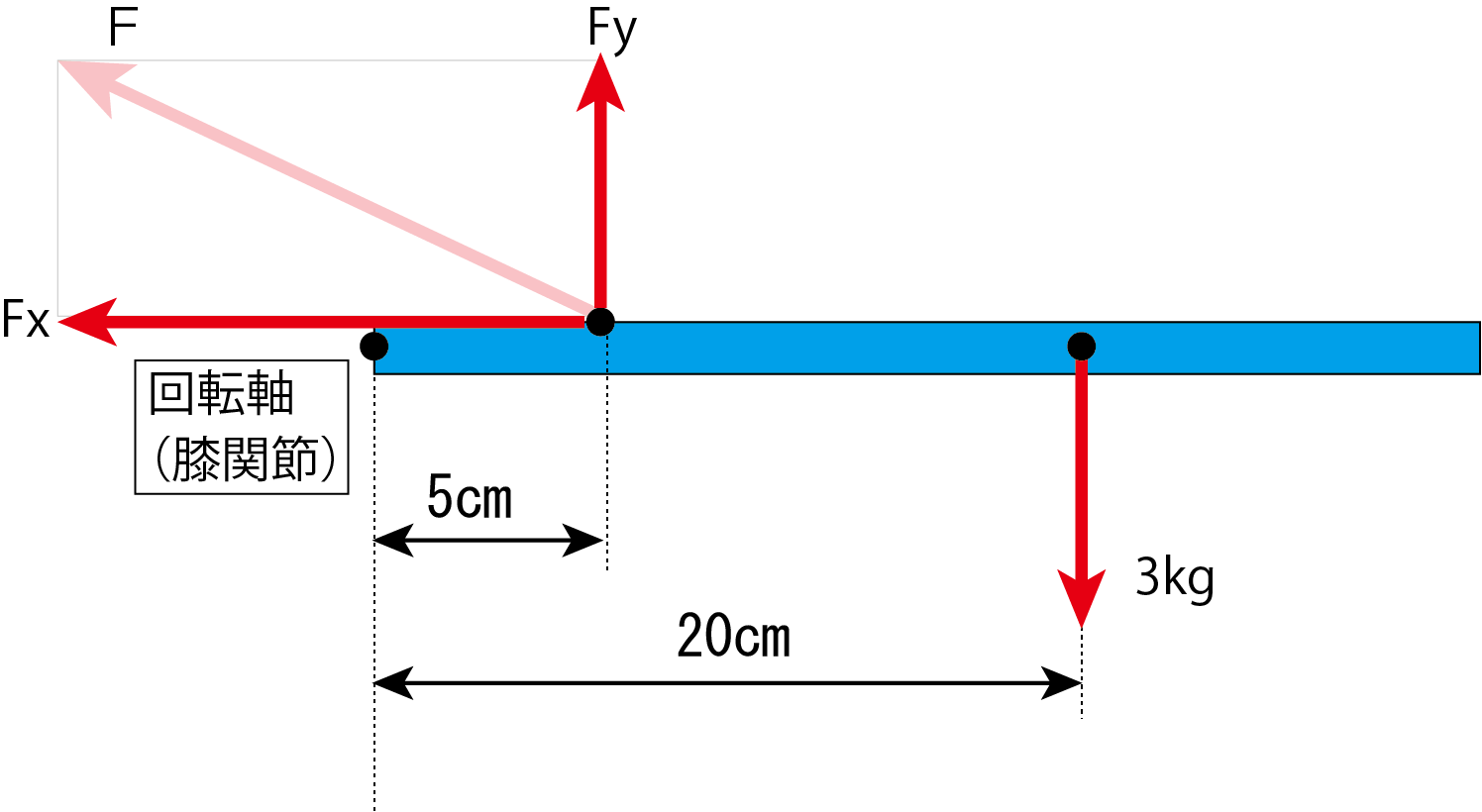
数値が入れてみました。「モーメントのつり合いの式」を立てることで、不明な大腿四頭筋の力を求めてみます。大腿四頭筋の力Fを垂直方向Fyと水平方向Fxの分力に分けています。

膝関節を回転の中心とし、時計回りの回転方向をプラスとします。
-０ cm × Fx - 5 cm × Fy + 20 cm × 3 kg ＝ 0
これを解いて、
Fy＝12 kg

さて、ここで本当に知りたいのは、分力Fyではなく、Fです。今、大腿四頭筋の力の方向がX方向から3０度傾斜しているとします。三角関数を使うと、FとFyの関係は次のように表せます。
Fy＝F × sin (30度)
三角関数表からsin (30度)は0.5です。F＝Fy ÷ sin (30度)、F＝12 kg ÷ 0.5からF＝24 となります。今回、大腿四頭筋の張力FはFyの２倍の２４kg（約240N）でした。肘を曲げてリンゴを支えているときの上腕二頭筋の力が１０kgほどでした。下肢の筋はこのような簡単な計算でも、大きな力が必要なことがわかります。

先頭に戻る