中央値(median)とは、データや集合の代表値の一つで、順位が中央である値のことです。データの個数が奇数の場合ば中央の値ですが、データの個数が偶数の場合は、便宜的に中央順位2個の値の算術平均としています。
代表的な統計指数で、歪度の大きい分布など非正規分布をしているなど場合にも適切な指標となり得ます。特に、いわゆる「外れ値」がある場合でも算術平均の様には影響を受けにくい特徴があります。臨床検査データなどは非正規分布を呈するものも多く、このため平均値(算術平均)を用いることは適切とはいえない場合も多々あります。一方、平均値ではなく中央値を採用すると、そのデータ分布は正規性がないと宣言していることになり、正規分布を前提としたt-検定などのparametric解析は適応することはできません。一般にparametric解析とnon-parametric解析ではparametric解析が検出力(有意な差がある場合に差があると検出する能力)が高いので、全ての解析で中央値を採用することは適切ではありません。測定値を対数化することなどで、母集団分布を正規分布に近い分布に変換するなどの工夫を行うこともまた重要です(この場合は幾何平均が代表値となります)。
データの中の数値の相対的位置をみるのに用いる数値のことで、例えば全テータを四等分したものは四分位数(Quartile)と呼び、百等分したものは百分位数と呼びます。分位数は分位点や分位値とも呼ばれます。臨床データの解析では四分位数を用いた解析が多いと思われますが、四分位数では下から25 %にあたる数を第1四分位数、50 %にあたる数を第2四分位数、75 %にあたる数を第3四分位数と呼びます。第2四分位数は中央値にあたります。
分位数の求め方にはいくつかの定義(流儀)があります。
(1)Tukeyの定義(オリジナル)
アメリカの数学者John Wilder Tukey(ジョン・ワイルダー・テューキー)が考案した方法です。Tukeyは右の図の様に、データを小さい方から階段状に並べ、途中で折り返し、中央値が最初の高さに戻ると、再び階段状に数字を並べ、最大値が再び最小値や中央値の高さに戻るように並べた場合の、最も低い点の数値をhinge(蝶番)と呼びました(数学者は「手術」とか「劇場」とか時々変な名前をつけます)。このhingeの部分が第1四分位数と第3四分位数になります。右の例では1〜13までのデータがありますが、中央値は7になり、第1四分位数は4、第3四分位数は10となります。Hingeの部分がふたつの数字となった場合(サンプル数が8以上の4の倍数では起こり得ます)は、それぞれの算術平均を取ります。Tukeyはこのふたつのhinge(第1四分位数と第3四分位数)と中央値並びに最小値と最大値を合わせて五数要約(five-number summary)と呼んでいます。
(2)文部科学省推奨の定義
これは中学高校の教科書に載っている四分位数の定義です。簡単に計算できるのでこの方法を文部科学省は推奨している様ですが、科学論文等にまで推奨しているものではない様です。この方法では、まず中央値を算出し、中央値未満のデータで中央値をとり、これを第1四分位数とします。また、中央値より大きいデータの中で中央値をとり、これを第3四分位数とします。中央値が複数のサンプルからなっている場合は、どれか一つのサンプルを削除するだけとなります。
サンプル数が偶数の場合はTukeyの定義で算出する値と同じになりますが、今回の例の様にサンプル数が奇数の場合には、微妙に異なる数値となります。
(3)Excelでの定義
四分位数はExcelの数列から関数機能を用いて算出することもできます。「QUARTILE.INC」関数と「QUARTILE.EXC」関数の二つがありますが、算出方法が少し異なります。「QUARTILE.INC」関数では最小値と最大値の間にある各サンプルの間隔(n-1個あります)を4等分することで、下から\({\cfrac{1}{4}}\)の位置が何番目のサンプルにあたるかを算出します。1〜14からなる14個のサンプルからなるデータを例にとると、下から\({\cfrac{1}{4}}\)番目の位置は\(1 + {\cfrac{1 \times (14 - 1)}{4}}\)番目のサンプル、すなわち4.25番目のサンプルが第1四分位数となり、下から\(1 + {\cfrac{3 \times (14 - 1)}{4}}\)番目のサンプル、すなわち10.75番目のサンプルが第3四分位数となります。小数点以下となるため、第1四分位数は4番目の値と5番目の値にそれぞれ0.25と(1-0.25)の重みをつけた算術平均(加重平均)を、第3四分位数では、10番目の値と11番目の値にそれぞれ0.75と(1-0.75)の重みをつけた加重平均を算出します。
一方「QUARTILE.EXC」関数では、最小値と最大値の外にある2つの間隔も考慮した計(n+1)個の間隔を4等分して「QUARTILE.INC」関数と同じ様に計算しています。
(4)4つの四分位数の定義の関係
どの計算法でも中央値は同じですが、サンプル数によって、4つの四分位数は一致したり異なったりします。
・サンプル数が偶数の場合 ・サンプル数が奇数の場合
「Tukey」=「QUARTILE.INC」≠「文科省」=「QUARTILE.EXC」
サンプル数が十分に大きく、また極端に飛び飛びの値でなければ、どの方法でも極端に値が変わるものではありません。しかし、どの方法で四分位数を算出しているのか、意識しておく必要はあります。
中央値や四分位数によるデータの分布を表すための表現法です。Tukeyによって提唱された方法で、中央値を「仕切り線」とした第1四分位数から第3四分位数までの「箱」を描き、「ヒゲ」を追加します。この「ヒゲ」の描き方にもいくつかの流儀があります。
(1)Tukeyの方法
第3四分位数(Q3/4)から第1四分位数(Q1/4)を引いた値を四分位範囲(interquartile range; IQR; IQR = Q3/4-Q1/4)と呼びますが、Tukeyの方法では、第1四分位数からIQRの1.5倍を引いた値から第3四分位数にIQRの1.5倍を加算した範囲の最小値と最大値の間に「ヒゲ」を引きます。この範囲外のデータは「はずれ値」として個別にプロットします。
(2)最大値と最小値をつなぐ方法
IQRと関係なく、最大値から最小値まで「ヒゲ」を引く方法です。簡単に作成できますが、「はずれ値」の情報を削除してしまう方法です。
(3)その他の方法
ソフトウェアパッケージの中には、百分位数の5%の点と95%の点を繋いだ「ヒゲ」を引くものなどもあります。
(4)箱ヒゲ図の実際
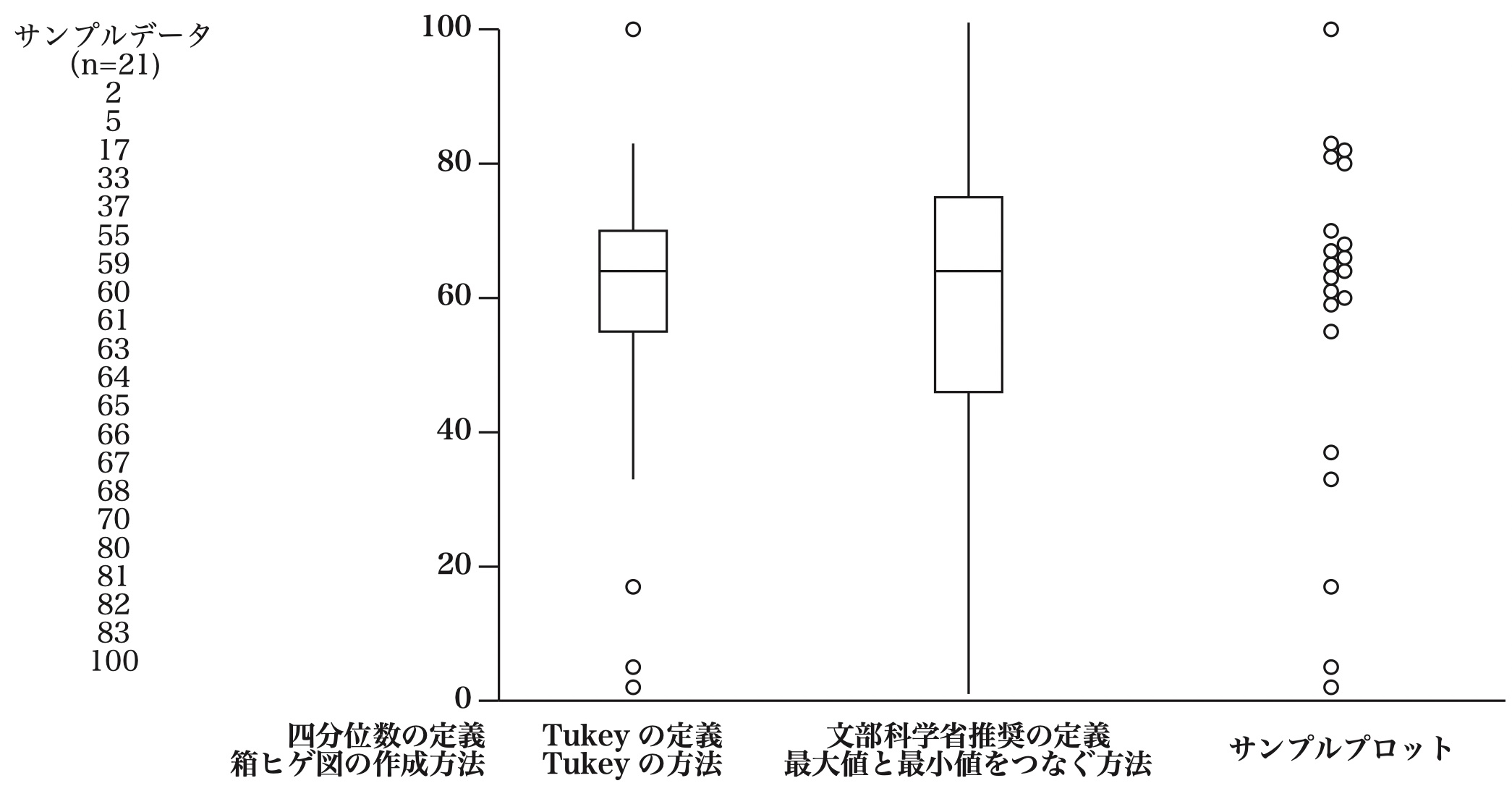
仮定サンプルで箱ヒゲ図を描いてみます。どちらも同じデータから作画していますが、四分位数の定義の方法や「ヒゲ」の引き方の違いで印象が大きく異なる図となります。作画する場合やグラフを理解する上で、どの様な方法でデータ処理及び作画されたのか、確認する必要があります。
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||