









����17�N�x�l���w�ȑ��ƌ���
�Ñ㊿�������@�\�������̋N���\
�i���{�e�͑��Ƙ_���Ɉꕔ�C�������������̂ł���j
02L1126R�@����z��@ �@�w�������F���[���
�����c�c���
���́@�ꂩ��l�̋N ���c�c�O��
�@ �@1�@���_�c�c�O��
�@�@2�@��c�c�l��
�@�@3�@��c�c�ܕ�
�@�@4�@�O�c�c�ܕ�
�@�@5�@�l�c�c�Z��
�@�@6�@�����c�c�Z��
���́@�܂����̋N ���c�c����
�@ �@1�@���_�c�c����
�@�@2�@�܁c�c���
�@�@3�@�Z�c�c���
�@�@4�@���c�c��Z��
�@�@5�@���c�c����
�@�@6�@��c�c����
�@�@7�@�����c�c����
��O�́@�\�����݂̋N ���c�c��O��
�@ �@1�@���_�c�c��O��
�@�@2�@�\�c�c��l��
�@�@3�@�S�c�c��ܕ�
�@�@4�@��c�c��Z��
�@�@5�@�݁c�c�ꎵ��
�@�@6�@�����c�c�ꔪ��
���_�c�c����
���c�c��Z��
�Q�l�����c�c����
�@���{�Ŏg�p����銿�����͒����Ő��܂ꂽ�B�������Ȃ���A�n�߂��猻�݂̎p�ł������킯�ł͂Ȃ��B�����ŌÂ̕����Ƃ����b������[1]�ƌ��݂� ���`�� �� ���͔@���ł���B��A��A�O�A���ɑ傫�ȈႢ�͂Ȃ����A�ق��͈قȂ�B�b�������Ȍ�A������⽕��Ȃǒ����Ԃ̎��̕ω����o�āA���݂Ɏ������B
�@�{�e�ł́A�b�������Ɍ����銿�����A����я���[2]�����ƂɋN����Nj��������B�������̋N���͍b�������A���邢�͍b���ȑO�̓��Е����ɂ܂ők ��B�l �@ �̗v�f�Ƃ��ẮA�b��������y��Ƃ��邪�A���łɉ�ǂ���Ă��铩�Е����������Ă݂����B�M�҂͊��������A������̑���[3]����A�\1�̎O�n���ɕ��ނ� ���B�����āA���܂��܂Ȑ������ƂɎ������q�ׂ����B
�\1�@�������̕��ތn���}
| �� | �� | �O | �l | �� | �Z | �� | �� | �� | �\ | �S | �� | �� | |
| A |  | 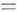 |  |  | |||||||||
| B |  |  | 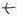 |  |  | | |||||||
| C |  | 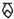 |  |  |
�@�������a������܂ł̌o�܂��ȉ���(2)�A(3)�ɋL������ŁA��|�̍l�@�Ɉڂ�B�_�q�̕����́A�e�͂Ƃ����̏����ɏ]���B
�i�A�j���_�F�e�n���ɑ����銿�����A���ׂĂ�ʂ��Ă̍l�@�B�@�Ȃ��A�ȉ��̂��Ƃ��}����߂�B�l���̌h�̂͏ȗ�����B�����҂�����ꍇ�͐������L���B����\���厚�i��A��A�Q�A�c�j��A�\���i�b�A���A ���A�c�j�\ �� �x�i�q�A�N�A�ЁA�c�j�A��i�Z�j�͈���Ȃ��B�b�������ɑ��݂������̌��^�ł����A��A�O�A�c�A�݂̏\�O�����݂̂�ΏۂƂ��A�㐢�ɑ������ꂽ���ȏ�̐� �ʂ͈���Ȃ��B�����̖��O��Ő��A�o�ŔN�A����ɒ���߂Ȃǂ̔ԍ��ł͎Z�p�������g�p����B�}���ɂ����Ă���O�I�ɁA�Z�p�������g�p���邪�A�ق��͈��p�� �����ׂĊ������ɉ��߂�B�{�e�Ŏg�p���銿���́AJIS�R�[�h�����ɂ����p�����E�l�� �p�����������Ƃ��A�Y�����Ȃ������͐������g�p�����B�u�c�� ���͂Ȃ��v�̂��Ƃ��\����p���邪�A���ׂĕM�҂̊nj��͈̔͂ɂ��B
�@�l�Ԃ̐��ɑ���F���ƌv���\�͂́A�ȉ��ɗ�L����i�K��ǂ��Ĕ��B�����B
�@�̐��ɑ��āA���i��j�ƗL�i��ȏ�j����ʂ���B�@�@����B�����̔F���A�C����E�͌v���\�͂ł���B��҂ł́A������ΏۂƖ��W�Ȃ��̂��A�u��Έ�Ή��v�����Đ������i���p������B
�@���B�̓r���ɂ́A�������T�O�Ȃǂ̐��ɂ܂��\���v�f�̂ق��A������̂Ɏg������⏬�Ȃǂ̓�����v���\�͂̔��B�ɉe����^�����B
�@���̗v�f�ł́A�ꂪ�d�v�Ȉʒu���߂�B�ꂪ�Ȃ���A���͈꒼����ɕ��ׂ������ɂȂ�B����Ɛ��̑����ɔ����A�L�������Ƃ��ʓ|�ɂȂ�B�� ���A���p �� �Ɍ�����̂��B�\�i�@�̏ꍇ�A�ꂩ���܂ł������Ƃ���Ȃ�A�\��S�Ȃǂ̈ʂ�\����͏c���ɂȂ�B���̓����ɂ��A���Ȃ�����Ŗ����ɐ���\���� ��p�ݏo�����̂ł���[4]�B
�@�l�Ԃ̌v���\�͂����B�������Ƃ́A�v�������ׂ����̋�������߂���B�L�^�E�ۑ��̒i�K�ւƈڂ�B�g��ꂽ�}�̂̎���́A�b����̖_�ɕt���� ������ �ځA���Ȃǂ���������B�����邾���łȂ��A���������ʂ��`�Ƃ��ĕ\���ł���悤�ɂȂ����̂��B
�@�������A�L�^����v�Z�̒i�K�ֈڍs����ƁA���ݖڂ⏬�ł͗p�������Ȃ��B�u�v�Z�v�Ɓu�i�v�Z�ߒ��́j�L�^�v���ɖ��������Ȃ�����ł���B�� ���Ő� �� �����ݏo���ꂽ�B�}�̂ɐ��������ނ��ƂŁA���Ȃ������Ŏv���ʂ�̐���\������p��g�ɂ����̂��B
�@�����̌`�͍����ƂɈقȂ邪�A��������ۑ������肷��̂Ɏg��������A���`�ɊW����Ⴊ������B���\�|�^�~�A�ł͔S�y�ɍ��܂ꂽ�����ь` �i�V�� ���[�������j�A���[�}�ł͖̖_�ɕt���ꂽ���ݖڂ̌`�i���[�}�����j�̂��Ƃ���ł���[5]�B
�@�ꂩ��l�܂ł̋N���ɂ͏���������B�Ƃ�킯���̎n�܂�ł����́A�Z���ɏ]���A�u�w�̏ی`�v�A�u�Z�Ԃ̏ی`�v�A�u�w���v�Ƃ���O���ɕ����� ��B���� �� ��ȏ�ł́A�u��Ӂv�̐��������B
�@�w�̏ی`�@�s�́A�ꂩ��l���A�\�����鐔�̕������L�����w�̏ی`�Ƃ���[6]�B�u���Â̐̂���A�������̏\�{�̎w�͂����ΐ��ϔO�̋�ۓI�Ȕ}�̂Ƃ��Ė� ������ �� ���v[7]�Ƃ���邲�Ƃ��A�w�̎g�p��������̂ɖ𗧂͎̂����ł���B�܂��A�w�ŕ\�������ʂ��A�����Ƃ��Ēu�����闬��͎��R�ł��낤�B����āA�{���� �M�ߐ��͍����Ƃ�����B
�A�Z�Ԃ̏ی`�@�����l�́A�v�����Ɏw�����łȂ��Z�Ԃ����g�p����������[8]�B�����́A����Z�Ԃ̏ی`�Ƃ���[9]�B�v������̎Z�Ԃ��A�\���������L�����`�� �Ƃ� ���B �Z�Ԃ́A�w�Ɠ��l�Ɏg�����߁A�{�����܂����R�ł���B
�@�O�q�̓���́A���ƂɂȂ�v������قȂ邾���ŁA������ۂ����_�ł͈�v����B
�B�w���@��ł���A�z���������ʂ̈���A��{�̐��ŕ\���l���ł���[10]�B�O�q�̂��Ƃ��A�������Ƃ́A������Ώۂ̐����Ɩ��W�Ȃ��̂ň�Έ�Ή� ������ �s �ׂł���[11]�B����āA�_��̈�{�������ʂ̈��\�����ƂɂȂ�B
�@�ȏ�̎O������{�ƂȂ邪�A���̐�������B����́A�O�q�̂����ꂩ��ł͂Ȃ��A�u�ی`�v�ł��u�w���v�ł�����ƍl����B�w�b�����ҁx�ɂ́A�ꂩ ��܂� �� �̐Ϗ�������B�܂͎�̎w�̖{���Ɉ�v���邽�߁A��̎w�̏ی`�Ƃ���B�܂��A�Ϗ����w���̂��̂ł͂Ȃ��A�����ے�������e�������߂ɁA�w���ł���Ƃ��� [12]�B
�@�@�@�}1�@�����܂ł̉ߒ�
�@�ȏ�A�l�����ȒP�ɏЉ�����A�����̉ߒ��������������ŁA�l�@�������B�����Ɏ���܂łɂ́A�K���\�����鐔�̑z��������͂����B���}�̌o�Ha �́A�z�� �� �����ځA���`������u�w���v�ł���B�o�Hb�́A�w��Z�Ԃ̌v���������đ�������u�w���ib1�j�v�Ɓu�ی`�ib2�j�v���B
�@���i�K�ł́A�����ꂪ�L�͂������肵���Ȃ��B�����A�v���������邩�ۂ��Ɋւ�炸�A�w������s���邱�Ƃ����͔��f�ł���B����āA�w�������� ���A�� �� ��l�܂ł̎��`�̌��^�ł���ƕM�҂͍l����B
�@�������A�N�����l����ɓ������ẮA�O�q�̐��ȊO�Ɏ��̋^���������B��������������ŁA�����ł����ȏ�͂����Ȃ鐔�ł��邩���B�u�w���v �u�ی`�v �� ���łȂ��u��Ӂv������Ƃ���l�������B�P���̈���܂߂āA�l���Ă��������B
�@�Ȃ��u��Ӂv���������ɓ�����A���̒�����z�u�ɒ��ڂ��A�Ӗ�������Ƃ��Ę_�q������͂Ȃ�[13]�B�������M�҂́A�w�b�����ҁx�Ɍ��鎚�`�̐� �̒��� �� �z�u[14]���A�u��Ӂv�Ƃ��Ė��Ӗ����ƒf��ł��Ȃ����߁A���ڂ��Ă݂����B
�@��́A�u�P���v�ł��邩��u��Ӂv�̍l���͔������Ȃ��B�{�߂ł́A���݂̗L���ɕ������Ƃ��́A�u�L�v�ɓ�����ŏ��̐��A��̎��`���l����B
�@����\�����߂ɁA�Ȃ�������p�����̂��B�܂��A���\���̂ɕK�����������łȂ��Ă��悢�̂ł͂Ȃ����B�܂��A���ł��闝�R���l���āA�c���̕����� �̖�� �� �����������B
�@�O�҂ɑ��āA�e�R����������B����̂��Ƃ��L���ł��\�����邪�A�~�`����`���Ӗ�����ƌ�����ꂩ�˂Ȃ��B����āA�s�v�ȊT�O��z�N�����Ȃ� �L����I �����ׂ����Ƃ���B����\���ɂ͓_�ł������x���Ȃ����A�w�I�ϓ_���猾���A�ʒu�݂̂Œ������Ȃ��B�܂�A���݊��Ɍ����邽�ߐ��ɂ����Ƃ��� [15]�B
�@���Ď���́A�e�R��������_�̒�`�ɓ��ӂ��邪�A�������ɈقȂ錩���������B�قƂ�ǂ̐l���A�u�E�v��u�C�v��_�Ƃ��ĔF���ł��邾�낤�ƍl�� ��� ���B �_���ڂɂƂǂ܂�ɂ����Ƃ��Ă��A�Ӗ�������A�F�������Ƃ���[16]�B�e�R�́A�_���F������ɂ��������뜜���邪�A������ɂ����������B���ł� �Ȃ��A�_�̐Ϗ��ł����Ȃ����ƂɂȂ�B
�@���́A�����ȓ_�������L���Đ��ɂ������߁A�ꂩ��l�͐Ϗ��Ȃ̂��Ƃ���[17]�B���Ƃ��Ƃ͓_�ł��������A���炩�̗��R�ɂ����ɂȂ����Ƃ��� �̂��� ���B�_�����ƂȂ������R�ɑ�����͂Ȃ��A�O�q�̉e�R�Ǝ���̐��ɂȂ炤�ق��Ȃ��B�_�ł����Ă��s�s���͂Ȃ����A���݂�c�����邽�߂ɂ͓_�����̕����� �ʓI���Ƃ���̂��A�ꂾ������������ł̕M�҂̐��_�ł���B
�@���ɁA��҂̕������̖��ɑ��ẮA�s����������B��̎w���g���Đ�����Ƃ��́A���ӎ��ɉE��ōs���A�ꂩ��l�܂Ŏw��|�����߉��������Ƃ��� [18]�B�������A�{���͎���g�����Ƃ��O��ƂȂ邽�߁A�}1�̌n��a�͖�������邱�ƂɂȂ�B�܂����\�������ɑ��āA�\��\���c�������邽�߁A�O�� �̖��Ɠ��^��͂Ƃ��ɏ\�ƍ��킹�đ�O�͂�2�Ō�q�������B
�@��ȏ�́u�����v�ł��邽�߁A�O�q�̂��Ƃ��A��ӂ��ۂ��̖�肪������B�b�������̎��`������ƁA��l�܂ł́A���ׂĉ��̈�{���ɂȂ炢�A�d �˂ď� �� �Ϗ��ł��邱�Ƃ��킩��B�܂́A�ꌏ�̂ݐϏ��̃T���v��������[19]�B
�@�C�t���[���������̊T�O[20]�ɏ]���A��͈�{��ƕ\�������B�܂�A�u��v�Ɓu��v�̉�ӂƂȂ�̂��B�������e�R�́A�u��v�Ɓu��v �̑g�� �� �킹�ɂ���ӕ����ł͂Ȃ��A�w���Ƃ݂�[21]�B
�@�@�i�A�j  �i�b�l�Z�j
�i�b�l�Z�j
�@�@�i�C�j  �i�S���O�E�l�j
�i�S���O�E�l�j
�@�@�}2�@�b�������́u��v�@�@�@
�@���`�����Ă݂悤�B�}2�́i�A�j�́A�����ɂ͓�{���s���Ƃ����������A�����͓������B�t�Ɂi�C�j�͕��s�����A�オ�Z���A���������B������ł� �邪�A �� �����قȂ�̂��B�����ɈӖ�������Ȃ�A��ƈꂪ�����ł���Ƃ͂�������[22]�B���ʂƂ��āA��͈�{��̒l�����A�i�C�j�̎��`����́A��̈ꂪ�� ���ł���Ƃ͎v���Ȃ��B
�@�ȏ�̂��Ƃ��A�����������ł��A���`�̍ו����قȂ�ꍇ������B��ӂ��w�����̖��́A�Ϗ��̎��`���ׂĂ������������Ō��_���o���B
�@�O�ɂ����Ă��A������肪������B�����u��v�Ƃ͈قȂ�A���Ɖ��̉�ӂȂ̂��̖��ł���B
�@�e�R�ɂ��A��ƈ�̉�ӕ����Ƃ���l������������[23]�B�����A�i�E�j�̂��Ƃ��z�u���ꂽ�u��v�Ɓu��v�̉�ӂ́A�����Ȃ�Ӗ������� ���B��� �� �{��Ƃ��Ă��A�Ȃ����킹��K�v������̂��B���^��ɑ�����͂Ȃ��A�M�҂̐��_�ɂ��ق��Ȃ��B
�@�@�i�E�j 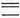 �i�s���j
�i�s���j
�@�@�i�G�j  �i�O�Z�E��E�O�j
�i�O�Z�E��E�O�j
�@�@�}3�@�b�������́u�O�v
�@�C�t���[�́A��Ɠ��m�炸�O���{��ŁA�l���{��ŕ\���������Z���̗���Љ��[24]�B�������������ł����Ă͂܂�ꍇ�́A�i�E�j�̂� �Ƃ��� �` �ɂȂ肤�邾�낤�B
�@�܂��O���A����O�{�ςݏd�˂��`�ŁA�u��v���O���킹����ӂ��Ƃ���l���͂ǂ����B�i�G�j�̂��Ƃ��A�������������A���ꂼ�ꂪ���Ԋu�ɔz�u���� ��O�{ �� ���ō\������鎚�`�ɓ�����B�O�q������̓����A���Ȃ킿��{��{��̌����ɂ��B�l�ނ��V���Ȑ������X�Ɛ��ݏo���_�@�ƂȂ肤��A�ł����n�I�ȊT�O�� �ЂƂł���[25]�B
�@�l����ӂƂ����ꍇ�́A�O�ʂ�̑��������ł��悤�B
�@��{�i��{��{��j�ƕ\���邾�낤�B�u��v�Ɓu�O�v�̉�ӁB�}4�i�I�j�̎��`�Ɍ�����z�u�B�@�@�i�I�j  �i�O�l�E���E�܁j
�i�O�l�E���E�܁j
�@�@�i�J�j 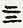 �i�O��E���E��j
�i�O��E���E��j
�@�@�i�L�j  �i�]��Z�E��j
�i�]��Z�E��j
�@�@ �}4�@�b�������́u�l�v
�@�@�͗����ɋꂵ�ށB��{�O�̕\�L�ɂ͉��̈Ӑ}�����������Ȃ��B�O�{��ł���A�\�����鐔�̒��O�ŗݐς���������v���A�V���Ɉ��������v�l�� ����� �� �������悤�B�����A�����@�ɈӖ�������Ƃ��v���Ȃ��B
�@�A�͑O�q�̎����Ɠ��l�ɍl������B
�@�B�̏ꍇ�́A�O�߂ŋ��������Z���̗�ɊY������B�������A����̒������قȂ�A��́u��v������\���������ƂȂ�B����̐l�����w�ƒ��w�ł� �낤 ���B ����ƁA�Ў�Ŏl�܂Ő�������Ƃ�����A����̎w��p���Đ����邱�ƂɂȂ�A�����Ɍ�����B
�@�i�L�j�͕M�҂̎�ςɂȂ邪�A���̒��������Ƃɂ���A�E������ɂ��ĐL�����l�{�̎w�̏ی`�Ɍ�����B�Ӑ}���ꂽ�̂��A���R�Ȃ̂��͕s���ł� ��B
�@�Ϗ��͊�{�I�ɂ́A�ꂩ��l�܂łɌ����鏑�@�����A�܂���O�I�ɑ��݂���B���݂ɘZ�ɂ͌����Ȃ��B�܂܂ő��݂������A������̂ɗp�����w�� �ی`�� �l ���Ă����������͂Ȃ��B�l�ɂ����āA�i�L�j�̂��Ƃ��l�{�̎w�̏ی`�Ɍ����鎚�`���A�w��z�N������B
�@��̊T�O�����݂������Ƃ���A��ӂ̊T�O�̑��݂��l������B�i�E�j��i�I�j�̂��Ƃ��A�e���̔z�u���ϓ��łȂ��A�z�u�ɈӖ�������Ȃ�Ή�ӂ� �l���� �� ���Ȃ��B�����e�R���̂��Ƃ��A�u�������ސl�̏K����̂��́v�Ȃ�A��{�O�̂��Ƃ���ӂł͂Ȃ����낤�B�������A��{��{��{��̂��Ƃ���T�O������ �ɂ�����ӂł���\���͎c�����B
�@��ӂł���ɂ���A�w������s���Ă���o���ꂽ�ꂪ���ƂɂȂ�B��͂�w�����A�ꂩ��l�܂ł̎��`�̌��^�ƂȂ�v�l���Ƃ�����B
�@���̒����̑���́A�@���Ƃ����������B��ł́i�C�j�A�l�ł́i�J�j�̂��Ƃ��A���̒����̓��ꂳ��Ă��Ȃ����`�����݂���B���̒�����ς��邱�� �ŁA���� �� ����ʂ������邩���q�ׂ�����Ȃ��A�M�҂����_���畂���Ȃ��B�Ӗ�������Ƃ͎v���Ȃ����A�Ӗ����Ȃ��Ƃ��f���ł��Ȃ��B
�@�ꂩ��l�̎��`�ł́A�w������s�������`�Ƃ���̂��A�M�҂̌��_�ł���B�u�ی`�v�Ȃ�A�v����������B�u��Ӂv�Ȃ�A�w�������^�Ƃ��Ēa ������ �� �������v�Z�̎v�l�ɂȂ�ƍl����B
�@�n���`�Ƃ͈قȂ�A�{�n���ł͎��`�Ɉ�т����K�����������Ȃ��B�����ł͏\�i�@���̗p����邪�A�����̎��`���������A�܂ň�������߁A �ܐi�@ �� �v�f������B�������ܐi�@�Ƃ͂����A�s�K���Ȍ`�ł���B���̂��Ƃ��K���I�ł���A�N���̉𖾂͍���ł͂Ȃ����A�s�K���Ȃ̂ō�����ɂ߂�B
| ��
�` | �� | �� | �O | 亖 | �~ | �~ �� | �~ �� | �~ �O | �~ 亖 | �b |
| �� | �� | �� | �O | �l | �� | �Z | �� | �� | �� | �\ |
�@���o�I�ϓ_����̌��������ŋc�_����͖̂��d�ł��낤�B�����̒i�K�ł��łɑ��݂����������e������\�����l�������B���`�ȊO�ɁA���������C ���[�W�� �� ���ڂ��Ȃ���A�l�@��i�߂�B�{�n���ɑ�����ܕ����ɂ����āA��т������͎��̎O���ł���B
�@�e�R���F�����Ɗ�ɕ�����B�Z�Ɣ��́A����̎w�̏ی`�B�܁A���A��ł́A�܂���̏ی`�B���Ƌ�́A�܂̌Ì`�~�̕ω��`[27]�B�@����ւ̎����͈ȉ��ɋL���B
�@�e�R�́A�����̏ꍇ�A�Z��\���̂ɎO�{�O�A����\���̂Ɏl�{�l�ƁA������l���������B�m���ɁA�����Ɗ�̎��`������ׂ�ƁA�����͍��E�Ώ�
�ő���
��
�{�Ȃ��߁A����̎�܂˂ƍl����̂������͂Ȃ����낤�B��������́A�e�R���l�����܂�[30]�͒P�Ȃ鉯���ɂ����Ȃ��Ƃ���B�܂��u �v�Ɓu�~�v�Ƃ̑��ΊW�����o�����A���������Ƃ���[31]�B�܂��A�Ў��
�������Ƃ���[32]���߁A�����p���āA�E��E����ƌ��݂Ɏw��L���Đ�
�����Ƃ͍l���ɂ����B���S�ɂ͔ے肵���Ȃ����A�M�҂͎�����Ɏ^������B
�v�Ɓu�~�v�Ƃ̑��ΊW�����o�����A���������Ƃ���[31]�B�܂��A�Ў��
�������Ƃ���[32]���߁A�����p���āA�E��E����ƌ��݂Ɏw��L���Đ�
�����Ƃ͍l���ɂ����B���S�ɂ͔ے肵���Ȃ����A�M�҂͎�����Ɏ^������B
�@�����͎�܂˂𐔂ɑΉ������邪�A��܂˂ɂ�鐔�̕\�����ɂ́A�ق��ɓ������[33]�A�����ꂪ�������������肵���Ȃ��B����āA��܂˂ɗR�� ����� �\ ���͂��邪�A�Ȍ�̍l�@�̑Ώۂɂ͂��Ȃ��B��܂˂ɂ��ƂÂ����������邾���ɂƂǂ߂�B
�@�����E���[�́A�u���t�i�����j�v�ɒ��ڂ��邽�߁A���䂪�l���鑢���܂ł̌o��[34]�ɋt��킸�A���R�ł���Ƃ�����B
�@�M�҂́A�ȏ�̎O���̒��ł͓����E���[����L�͎����A���ꂼ��̊������ɑ�����������čl�@��i�߂����B
�@�����E���[�́A���ʂ̌܂�ngag�Ə̂����Ƃ���B�Ў�̎w�Ő�����ꍇ�A�ܔԖڂ̏��w���܂�Ԃ��ɓ�����B���̕����Ő����n�߂��Ȃ�A�܂��� �Ɂ��� �� �����]������B�܂�܂́u�N���X����v�C���[�W�������A���`�����ā~�ƕ\����������[35]�B�����u�����v�����݂��A�܂������ɓ������ʂ������ ��B�Ⴆ�Έꂩ���ɂ����Č܂́A�ꂩ��l�ƁA�Z�������Ȃ��ڍ����ɓ�����B�܂��A���@��p�����O�~�O�̖��@�w�ł���ɒ����ɔz�u�����[36]�B�� �ʂ̐����Ƃ��Ă��A�����i�����_�j�ɂ���̂��B���������l�X�̐��ɑ���F�����A�����قǂ��͕s���ł���B�������A���������l�X�����T�O������Ă���A �u�N���X�v���Ӗ�����\���͍��܂邾�낤�B
�@�k�́A�u���߁v�́u�߁v�̖{���ł���Ƃ���B�߂Ɠ����ŁA�����ꂽ�Ƃ݂�̂�[37]�B�����E���[�ɂ��A�߂��܂������̈Ӗ����܂ނ������B
�\��x
��
�́A�O���ƌ㔼�Ƃ���������|�X�g�ɓ����鎵�Ԗڂ�\�����ɓ��Ă�������[38]�B�k���ł́A�߂��܂��Â����瑶�݂��邱�Ƃ������ƂȂ邪�A�����ꂪ��
������f��ł��Ȃ����߁A�@���Ƃ���������[39]�B�����A���Е����̌܁i�~�j�ƍb�������̌߁i �j�Ƃ͈Ⴂ������B�b�������̌܁i
�j�Ƃ͈Ⴂ������B�b�������̌܁i �j�ƌ߁i
�j�ƌ߁i �j���ׂ����߂ɁA�{���̂��Ƃ�������
��������Ƃ��l������B
�j���ׂ����߂ɁA�{���̂��Ƃ�������
��������Ƃ��l������B
�@���́A�Õ��̌܂��A�Ϗ��� �ł���Ǝ���[40]�B����́A���̎O�{���~�ɕς��A�㉺
�̐��ƌ��������Ƃ���[41]�B���Ƃ��Ƃ͐Ϗ���
�ł���Ǝ���[40]�B����́A���̎O�{���~�ɕς��A�㉺
�̐��ƌ��������Ƃ���[41]�B���Ƃ��Ƃ͐Ϗ��� �����A亖�Ƃ̋�ʂ̂��߁A���̐����~�ƕ�
�`����������ɂȂ�B�����������Ƃ��āA���ʂ̎O���~�ŕ\�L����Ȃ���Ȃ�Ȃ����߁A���S�ɂ͔ے肵���Ȃ����A
�m�肵���������ł���B
�����A亖�Ƃ̋�ʂ̂��߁A���̐����~�ƕ�
�`����������ɂȂ�B�����������Ƃ��āA���ʂ̎O���~�ŕ\�L����Ȃ���Ȃ�Ȃ����߁A���S�ɂ͔ے肵���Ȃ����A
�m�肵���������ł���B
�@�Ȃ��A�㉺�̓�{���͉����������̖�肪�c�邪�A��猒��w�������w�ʎj�E��Ó��ܑ㊪�x�ɂ����������B�b���ȑO�̓��Е����ł́A�܂́~�ł��� �������B �܁i�~�j�Ǝ��i�{�j�Ƃ̍���������邽�߂ɁA�܂̏㉺�ɐ����������Ƃ���[42]�B
�@���`������A���������Ƃɂ����u�N���X�v�̃C���[�W�Ƃ����������B�O�q�̂��Ƃ��A���ʂ̐������l������́A�w�����Ƃɂ��铡���E���[�����L�͂�
�낤�B
�{
���������܂̈Ӑ}�́A���Е����̎��`�ł���~�ƈ�v���邽�߁A�m��ɒl����B�Ϗ��̌܂��w�̏ی`�ł���Ȃ�A亖�Ƃ̋�ʂ�e�Ղɂ��邽�߁A�w�̖{���ƌ�
�̃|�X�g�ɒ��ڂ������ʁA �̎��`�ɂȂ����ƕM�҂͍l����B
�̎��`�ɂȂ����ƕM�҂͍l����B
�@�����E���[�́A����͂Ȃ����A������Ƃ��̎�Ɖ����̌������Ƃ���B�܂܂Ŏw��܂�A�e�w�𗧂Ă�̂��Z�ł���B���̎p�͐���オ�����`�ƂȂ�A ���◲ �� ���ꌹ��liok�ŁA���̘Z�ɖ��������B��������オ��C���[�W������p�����Ƃ݂�[43]�B�������{���́A�܂܂Ŏw��܂�A�Z�̂Ƃ��ɐe�w�𗧂Ă鐔�� �����O��ƂȂ�B�Z�́A��̈ʂɂ����Ď��̂��Ƃ��ʒu�Â�����B��̎w�Ō܂܂Ő������ꍇ�́A�Ў�ň�ʂ萔���I���āA�܂�Ԃ��̈�ɓ�����B���ɗ��� �Ő������Ƃ��Ă��A��͂���̈�ɓ�����B������ɂ���V���Ɉ�{�w���o���A�܂�u����オ��v���߁A���i����オ��C���[�W�j�ɂȂ��邾�낤�B
�@�ٌ��ł́A�����A�u���v����āu�Z�v�Ƃ����Ƃ���[44]�B���́A ���Z�̂��Ƃ��Ƃ̎��`�ŁA���Ƃ̍������
���邽�߂�
���Z�̂��Ƃ��Ƃ̎��`�ŁA���Ƃ̍������
���邽�߂� �A
�A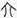 �Ȃǂ̎��`�ɕς����Ƃ���[45]�B���Ē��́A�b��������
�����āA�u�Z�v��
�u���v�Ɠ��l�Ɂu
�Ȃǂ̎��`�ɕς����Ƃ���[45]�B���Ē��́A�b��������
�����āA�u�Z�v��
�u���v�Ɠ��l�Ɂu �v�̌`�ō��܂ꂽ�Ƃ���B�����A�������邱�Ƃ͂Ȃ��Ƃ���[46]�B�ȏ�O��
�́A����������ƘZ���֘A�Â���������A���͐��ʂ̘Z��z�N������̂��B���^
��ɑ�����͂Ȃ��B�u���`�����邽�߁v�����ł́A�������ɂ����Ȃ����낤�B���Ɏw�Ő�����Ȃ�ǂ��ł��낤���B�܂ł��ׂĂ̎w��L���I���A�Z�͐e
�w���Ȃ��鐔�����ɏ]���Ƃ���B���������ł́A�L��������I���A�Ȃ���ŏ��̐��ƂȂ�w�𒆂ɓ����A���Ȃ킿�u���v��z�N�����邾�낤�B
�v�̌`�ō��܂ꂽ�Ƃ���B�����A�������邱�Ƃ͂Ȃ��Ƃ���[46]�B�ȏ�O��
�́A����������ƘZ���֘A�Â���������A���͐��ʂ̘Z��z�N������̂��B���^
��ɑ�����͂Ȃ��B�u���`�����邽�߁v�����ł́A�������ɂ����Ȃ����낤�B���Ɏw�Ő�����Ȃ�ǂ��ł��낤���B�܂ł��ׂĂ̎w��L���I���A�Z�͐e
�w���Ȃ��鐔�����ɏ]���Ƃ���B���������ł́A�L��������I���A�Ȃ���ŏ��̐��ƂȂ�w�𒆂ɓ����A���Ȃ킿�u���v��z�N�����邾�낤�B
�@���`���܂ň�����������ł́A�Z�����̈�ɂȂ邱�Ƃ͊m���ł���B�ܖ{�̎w�������Ў�����l�ɑz�N�����邾�낤�B�܂�Z�́A�V����
�u�ċ���
��v�|�X�g�ɂ��鐔�ʂŁA����オ��C���[�W�������A �̂��Ƃ����`�ɂȂ����ƕM�҂͌��_�Â�
��B
�̂��Ƃ����`�ɂȂ����ƕM�҂͌��_�Â�
��B
�@�����E���[�́A�c�_�����_�Ő邳�܂̏ے��Ƃ݂�B���́A��Ǝ��ł�������ꂸ�A�ق��̐��Ŋ���ƒ[�����o�邽�߁A��߂Ɠ��ꌹ�̌��t�� ts�fiet �ƌĂB���Ĕ��[�Ȃ��̂��o��}�Ăł��邻����[47]�B�{���ł́A�����̎����ɏ��@�̊ϔO�����݂������ۂ��̖�肪������B����́A�w�Ōv�Z�E�\�� ��������ɁA��@�ⓙ���̊T�O�����݂������͋^�킵��[48]�Ƃ���B���������l�X�̌v�Z�\�͂��A�����قǂ���_�q��������Ȃ��A�����ł��Ȃ����ł� ��B�����A�u�����v�Ȃ�Ή\�ł͂Ȃ��낤���B�l�Ԃ͎�������A�݂��ɓ���������ςނ��炾�B���͓����ł��Ȃ���őf���ł�����B�������A��� �܂͎w��z�N�����邪�A���͂Ƃ�킯�����z�N�����Ȃ��B�����E���[���́u���[�Ȃ��̂��c��v�C���[�W�ł���B
�@�т́A�Â���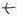 �Ƃ����Ƃ���B�u�v�̌Õ��ł��邻����[49]�B�Ǝ��ɂ́A�����Ȃ�W
������̂��B��͂萔�ʂƌ��т���K�v������B�u�菝�̌`�v�ł��邽�߁A
���[�Ȃ��̂��c��C���[�W�Ƃ��铡���E���[���ɋA�����邾�낤�B
�Ƃ����Ƃ���B�u�v�̌Õ��ł��邻����[49]�B�Ǝ��ɂ́A�����Ȃ�W
������̂��B��͂萔�ʂƌ��т���K�v������B�u�菝�̌`�v�ł��邽�߁A
���[�Ȃ��̂��c��C���[�W�Ƃ��铡���E���[���ɋA�����邾�낤�B
�@�����f���ł���A���肫��Ȃ��������A���Ďc�肪�o��C���[�W�ɂȂ������ƕM�҂͍l����B��͂�u�v�Ƃ��W������B
�@�����E���[�́A�����l����Ǝ��X�ɓ��������i�������j��������A���E�����ɔw���ĕ�����邳�܂��ے��������}�`�ł���Ƃ���B�܂��A�ʂ� ���Ɠ� �� ����puat�ƌĂсA�ʂ��C���[�W�̂��鎋�o�L���ŕ\�L����[50]�B�O�߂ŋ����������̎v�l�ɏ]���A���͎��X�Ɠ����ł��鐔�ŁA�ʂ��C���[�W�ɂ� �Ȃ���B
�@�����u�́A���̖{�`���u������v���Ƃ���B�ʂ��ی`���肽�w��������������[51]�B���́A�ʂ�邳�܂��A�`�̂Ȃ����ۓI�ϔO�ł��邱�Ƃ� ��A�w�� �� �ی`�ƌ��Ȃ��B�N���͋�̓I�Ȃ��̂ɊW���A���r��L�����`��A�e�w�Ɛl�����w�𗣂��ĐL�����`���ƍl����[52]�B�n�́A�����]�̍ŏ��̎��`���Ƃ� ��B�����]�͓������B�̗̂��e�ɂ����]�i�r�j���A���ʂ�\���ŏ��̕����Ƃ������߁A���ʂ̍ŏ��̕����ł����邻����[53]�B�ȏ�O���ɂ����ẮA�w���� �̂��ی`�Ȃ̂��̖�肪�c�邪�A�}1�̌o�H�Ɠ��l�̐}���ʼn��������B�z�������u�ʂ��v�C���[�W�Ɏn�܂�A�̗̂��e�ɂ���r����邩�ۂ��Ɋւ�炸�A ���`������闬��ł���B���ʂ̐������A�����l����Ɓu�ʂ��E�����ɂȂ�v�C���[�W�ɍ��v����B
�@���̍l���͂ǂ����낤���B�N���X�i�~�j�����݂��邽�߁A�g�ݍ��킹����{���̐悪�l������B�����A�l�����̊T�O�����݂�����������Ȃ��B���� ������ �� �l������A�����p�̊T�O�܂Ŕ��B���Ă����\�������邾�낤�B���������l�X�Ɂu���́v�̈ӎ�������Ȃ�A�������͂Ɂu�U��U��ɕʂ��v�C���[�W�̏ے� �����Ƃ��Ă����������Ȃ����낤�B
�@������ɂ���A�u�ʂ��v�C���[�W�̏ے��L���ł���ƕM�҂͍l����B
�@�����E���[�́A�I���Ȃ����}�`�Ƃ��邪�A�I�̈ӂ͂Ȃ��������B�u�Z�v�Ɠ��l�ɁA���ۓI�Ȑ�����������@�ł���B��͈�̈ʂōŌ�̐��ł���B ����K �� ���ꌹ��kiog�Ɩ��������B��͕I���Ȃ���p�����A�܂������s���Ȃ��ŋȂ���A���邢�͏I�ǂ��Î�������Ƃ���[54]�B
�@�т́A���Ȃ��{���̈Ӗ��ŁA��Đ����̋�Ƃ����Ƃ���[55]�B���́A���Ƃ��ƕI�̎��ŁA�r�̐߂��ۂ����Ƃ���[56]�B�n�́A�I�̍ŏ��̕��� �ŁA�� �` ���w�����Ƃ���[57]�B��͂�A�}1�̌o�H�Ɠ��l�̐}���ʼn��������B��̈ʂł͍Ō�̐��ł���A����ȏ�͐i�߂Ȃ����܂�̃|�X�g�ɂ���B�I�ǂ̃C ���[�W������A�I����邩�ۂ��Ɋւ�炸�A���`������闬��ł���B
�@�Ƃ���ŁA�Ȃ���Ώۂ�I���Ƃ���̂͂Ȃ����B���F��͒��̐����Љ��B���́A�u�I�v�͐́A�u肍�v�ł������ƍl���邻�����B  �̑O����
�̑O���� �́u���v�Ɠ����ŁA���̐����Ȃ��Ăł���
���ȕ����A�I�̏ꏊ�������Ƃ݂�B
�u��v�Ɓu���v�͎��`���߂��A�u���v�Ɓu���v�͒ʂ���B�I�̏ی`����Đ�����
��ɓ��Ă��Ƃ���[58]�B�I����āA��ɓ��Ă����R�͘_�����Ă��Ȃ��B�����������E���[���������Ƃ��A�オ��̈ʂ̏I�ǁA���Ȃ킿�u�܂�Ȃ���v�|
�X�g�ɂ��邽�߂ł���Ƃ����悤�B
�́u���v�Ɠ����ŁA���̐����Ȃ��Ăł���
���ȕ����A�I�̏ꏊ�������Ƃ݂�B
�u��v�Ɓu���v�͎��`���߂��A�u���v�Ɓu���v�͒ʂ���B�I�̏ی`����Đ�����
��ɓ��Ă��Ƃ���[58]�B�I����āA��ɓ��Ă����R�͘_�����Ă��Ȃ��B�����������E���[���������Ƃ��A�オ��̈ʂ̏I�ǁA���Ȃ킿�u�܂�Ȃ���v�|
�X�g�ɂ��邽�߂ł���Ƃ����悤�B
�@���c�́A�\�̉�����ω������ċ���������Ƃ���[59]�B���������́A�傫�Ȑ����珬���Ȑ����ł����ƍl����̂́A�����ɍ���Ȃ��Ƃ��� [60]�B ��� �ď\�̎��`����ɂ���A��ɕό`�������ċ���������Ƃ͍l���ɂ����B
�@��͂�\�i�@�̒��������ɂ����āA��͈�̈ʂŏI�ǂ̃|�X�g�ɂ���B��ɐi�߂Ȃ����܂�Ƃ��āA�Ȃ��肭�˂������`�ƍl����B
�@�{�n���ł́A�M��̏��Ȃ����ڗ���[61]�B�P�ɁA�Ӗ������������ɁA���Ȃ��M��̎��`������A���Ƃ����\���͔ے�ł��Ȃ��B���n����̐l�X ���� �� �Ƃ��A���ڂ���������Ή��̖����Ȃ����炾�B�w��p����ꍇ�����l�ł���B�������������ł���A�A���t�@�x�b�g�̂k��s�A�u�̂��Ƃ��A���b���ɍ��� �₷�����`�Ƃ������낤�B��̂��Ƃ����݂ɂ����Ǝv����Ȑ��A����ɂ��ꂼ�ꂪ�����I�Ȏ��`�ł��邽�߂ɁA���炩�̈Ӗ�������Ƃ���̂��Ó����B
�@�u���Ȃ��M��v��O��Ƃ��āA�����̂��C���[�W���琔�ʂɓ]�p�����ƕM�҂͍l����B�����̃C���[�W�Ɛ��̐�߂�|�X�g�́A���ꂼ��藣������ ���ł� ���A���҂������Ƃ������ƂȂ�B�Ȃ��A�ꂩ��l�̎��`�Ɣ�r����ƁA����g�p�����ۂ͉�����B�������A���S�ɂ͒E�p���Ă��Ȃ��B
�@��T�O�ɂ���Đ��ݏo���ꂽ�A�ʂ�\���������ł���B
�@�\�ł́A���͂�2�Ŏc�����A�_�ł͂Ȃ����ŕ\�L����闝�R��A�c���̖��ƍ��킹�čl�������B�S�A��A�݂ł́A���̈�{���̗L���A����ɐ����� ��ꍇ �� �����Ӗ����邩�����ƂȂ�B�w�b�����ҁx�ɋL�ڂ�����S�A��A�݂̎��`[62]�ƁA���̗L���ɕ������Ƃ��̌������}�ɍڂ����B
�@�@�S�̎��`�i�v27�j
�@�@�i�N�j 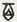 �i�b�O�Z�ꎵ���j�F24
�i�b�O�Z�ꎵ���j�F24
�@�@�i�P�j 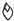 �i�O�Z�E�l��E���j�F3
�i�O�Z�E�l��E���j�F3
�@�@��̎��`�i�v16�j
�@�@�i�R�j  �i�b���Z���j�F16
�i�b���Z���j�F16
�@�@�݂̎��`�i�v19�j
�@�@�i�T�j  �i�������Z�j�F1
�i�������Z�j�F1
�@�@�i�V�j  �i�O�O�E�O�Z�E�܁j�F18
�i�O�O�E�O�Z�E�܁j�F18
�@�@�}5�@�w�b�����ҁx�̕S�E��E�݂̎��`�i�Z�p�����͕������j
�@�S�ł͂قƂ�ǂɁA��ł͂��ׂĂɁu�\�v���t����Ă���B�t�ɁA�݂ł͕t���Ȃ��̂��ʗ�ƂȂ�B�����ɑ��ẮA��̈Ӗ��Ƃ�������قƂ�ǂł�
��B�b
��
�����ł́A�\��ȏ�ɂ����č������p�����邽�߁A���ɓK�����Ƃ�����B�݂ɂ͑���������t����Ȃ����A���ɂ��A����\���݂ɂ͉������t����A�l����
�n����\���݂ɂ͕t����Ȃ��Ƃ����B�܂��O�҂͎g�p�Ⴊ���Ȃ��A��҂͑���������[63]�B����ɁA��S�ł����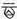 �̂��Ƃ��u��v���t����邱�Ƃ���A�u�\�v�͈��\���Ƃ�����B
�̂��Ƃ��u��v���t����邱�Ƃ���A�u�\�v�͈��\���Ƃ�����B
�@�\�͓��ʂȈʒu���߂�B��͈�̈ʂł͏I�ǂ̐������A�\�͗���̎w�̖{���ł���A����̎w�Ő�����ꍇ�A��͂�ɂ݂̐��ɂȂ�B�������\�i�@�� �́A�� �� �����܂Ƃ߂��V�����ʂ�\�����ł���B�܂�A�I���ł�����肩�A��̎n�܂�ł�����|�X�g�ł���B�\�̋N���́A�ȉ��̓���ʂ���l����B
�i�@�j��Ƃ̕������ɊW����
�@�e�R�́A�\�͍Ō�̐��ł��邩��A�ŏ��̐��́w��x�ɑ��ĒP�ɕ����������āb�Ƃ��ď\������킵���Ƃ���[64]�B�܂�������200�ŁA�S�̍� �ڂ� �u�\ �i�@�ōs���Ώ\�ʂɂ����Ă͈�i�}�}�A�\�j���͂��߁v�Ƃ���A��Ə\���֘A������B�\�͏\�i�@�ɂ������Ƃ��Ă悢�B�����ŁA��Ƃ̍���������邽�ߕ��� ��ς����Ƃ����B�������������ł���B��Ƃ̍���������邽�߁A�c�����Ƃ���������[65]�B
�@�n�́A��Ő������Ƃ��̎w�̋Ȃ��L���ɂ��Ƃ���B��͋Ȃ����w�Ȃ̂ʼn��A�\�͐L�����w�Ȃ̂ŁA�c�Ƃ���[66]�B�͂��߂�����������Ӑ}�� �đ��� �� ���̂ł͂Ȃ��A�w�ɂ�鐔�����̑���ɗR������Ƃ����B���ʓI�ɂ͕������̖��Ƃ����邽�߁A�i�@�j�ɑ�����Ƃ��悤�B
�i�A�j��Ƃ̕������ƊW�Ȃ�
�@����́u�������ꂽ��̌`�̏ی`�Ƃ��āA�w�b�x�Ƃ������`���p����ꂽ���̂ƍl������v[67]�Ƃ���B�����A�������c�ɍ��킹���Ƃ��̏ی` ���A���� �� �\�ł���Ƃ���B�܂��A�����̎w�̖{���͏\�ł��邱�Ƃɒ��ڂ��Ă���[68]�B
�@�����E���[�́u�\�i�@�ł͏\�͐V�����ʂɂȂ�v�A�܂��u�w�\�x�͍b�������ł͏c�̈���Ŏ������B���̈���́w��x�ƑΏ̓I�ł���v[69]�Ƃ� ��B�� �� ���A�������Ƃ͊֘A�Â����A�E�i���킹�W�߂�j�Ɠ��ꌹ�ŁA�ꂩ�������킹�܂Ƃ߂��C���[�W�Ƃ���[70]�B
�@�ȏ�̎O���́A���̂��Ƃ������Â��邱�Ƃ��ł���B�܂��A���킹�W�߂�C���[�W������B�����āA���C���[�W�ɂ��ƂÂ����ۂ��Ɋւ�炸�A�̐��� �\�ɗR �� ����Ώۂł��闼���̎w��I�сA�������ۂ�u�b�v�ɂ����ƕM�҂͍l����B
�@���āA�u�\�v��u�b�v�̂��Ƃ��A�_�ł͂Ȃ����̖��ƁA�c���̖����l�������B���҂̂������Ȃ��Ƃ�����ɓ_��p����Ȃ�A�ȉ��̕\�L�@���l�� ���� �� �낤�B
�@�u�E�v����A�u�E�v���\�Ƃ���B�@�@�ł���Ύ��`�����������ɁA�Ƃ��ɐ����ł���A�p�@�̔��ʂ������Ȃ��B����ĕ����Ƃ��Ă͖𗧂��Ȃ����߁A�g�p�����Ȃ��B�A�ƇB�́A��Ə\ �̈�� �� �_�A��������Ƃ���B�Ƃ��ɋ�ʂł��邽�ߕs�s���͂Ȃ����낤�B�܂����Е����ł́A�܁i�~�j�Ǝ��i�{�j���������₷���ƁA�O�͂�2�Ř_�������Ƃ��A�� �i�\�j�Ə\�i�b�j���܂��������₷���B����Ĉ�����_�A���������Ƃ����������������s�����悢�B�������A���ۂ̎��`���u�\�v�u�b�v�̂��Ƃ��_�ł͂Ȃ��� ��A���R�ł͂Ȃ��Ӑ}�I�ɓ_�̎g�p��������ƍl������B
�@�O�q�������A����͓_�ɂ́u�_�v�̈Ӗ�������Ƃ���B�����A�u�E�v�Ɂu��v�̈Ӗ�����������Ƃ��Ă��A�O�҂͖����A��҂͐����ł���p�@�͈ق� ��B��� �� �b�������ł́A�������画�f�ł��A�s�s���͂Ȃ��B���Е����ɂ����Ă��A�_���u�_�v�̈Ӗ��Ƃ��Ă͗p���Ȃ����낤�B�_��p���ĕs�s����������Ȃ�A��͂� �e�R���뜜����_�̑��݊��̌��@�ɂ��ƕM�҂͍l����B
�@�Ƃ���ŁA�c������܂�A�������画�f������b�������Ȃ�Ζ��Ȃ����A�����݂̂��_�݂��铩�Е����ł́A�c���̋�ʂ͉\�Ȃ̂��B�s�\�Ȃ�
�A�g�p
��
���Ȃ��B�������A��猂ɂ��A�����̐V�Ί펞�㖖���̓�\��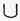 �A�O�\��
�A�O�\��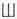 �̂��Ƃ��L����邻����[71]�B��A
�O�Ƃ̍����͔�������B���Ƃ́A���
�\�̋�ʂ̖��ɂȂ邪�A��������������p�͂Ȃ��A�u�\�v�Ɓu�b�v�̍�����
�������Ȃ��B
�̂��Ƃ��L����邻����[71]�B��A
�O�Ƃ̍����͔�������B���Ƃ́A���
�\�̋�ʂ̖��ɂȂ邪�A��������������p�͂Ȃ��A�u�\�v�Ɓu�b�v�̍�����
�������Ȃ��B
�@�M�҂͑��͂�2�ŁA�_�ł����Ă��s�s���͂Ȃ��Ƃ����B�������A�\�ƍ��킹�Č������Ă͂��߂āA�c���̕ω��݂̂ň�Ə\�̗�����\���邽�߁A���� ������ �� ���Ƃ�����B�������̗v�f�́A���Е����ł͍����̌����ƂȂ邪�A�b�������ł͗L���ɐ�������Ƃ�����B
�@�S�ȏ�ł́A�̍����Ƃ�����������B
�@�����E���[�́A��Ɣ��Ƃ̍����Ƃ���B���͂ǂ�̏ی`�����ŁA�����̏ے��Ƃ��ė��p�����Ƃ���[72]�B�M�҂̊��o�ɂ�邪�A�S���̌̂�� �̑O�� �� ��u��������v�Ɗ����邾�낤�B
�@�e�R�́A��Ǝ��Ƃ̍������Ƃ����B�\�i�@�ł́A�S�ʂɂ����ĕS�����ɑ�������B�n�߂̈ӂ������ƈ�Ƃ̑g�ݍ��킹�Ƃ���B���͎��̏ȗ��`�ł� ��Ƃ� ��[73]�B�S�ʂɂ����ĕS�����ɓ�����̂͊m���ł��邪�A�\�ʂł͏\�����ƂȂ肤��͂����B��ʂ��݈ʂł����l�ɂ�����B����āA���ł���Ƃ͂��� �� ���B
�@����́A�ꂪ��̎w�̏ی`���Ƃ���Ȃ�A���肵���`��̒܂ł��낤�ƍl����B�l�Ԃ̑̂ɏ\���݂��邱�Ƃ���A�u���̎w�̏ی`�ł���A�v�� �̎�i �� ���āw�S�x�ɗ��p���ꂽ���́v[74]�Ƃ���B�w�Ő��������������邽�߁A�{���̂��Ƃ���̎��ɁA�����l����̂����R���낤�B���̎w�ɂ�萔�������ۂ��� �s�������A�\�{�w�̓_�ł͋��ʂ���B
�@�ق��ɂ��A�ȉ��̎l��������B�������A��������������L����Ă��Ȃ��B
�@���́A�N�����@�̌`�ɂ���Ƃ���[75]�B�u�@�v�́w�����������x�A137�łɁA�u�]��畀�v�Ƃ��邲�Ƃ��A����畀�����킹���`�ł���B�M�҂́A�S �̋N�� �� �� �ł͂Ȃ��Ƃ��邽�߁A���ɏ]���@���W���Ȃ��ƍl����B�܂����ʂ̕S���A�@�ɓ��Ă�K�v�������������Ȃ��B
�@�́A�����Ƃ��Ďg��ꂽ�L�̌`���Ƃ���[76]�B���j�]�́A�K�܂̌`�Ɏ��Ă���Ƃ݂�[77]�B�����Ƃ��A�����ɊW������Ƃ��邪�A�Ȃ����� �̕S�� �� �Ă�ꂽ�̂��낤���B�L�̌`�A�K�܂̂�����ɂ������`�ŁA�g�߂ȑ��݂��낤���A���ʂ̕S�Ƃ̊֘A�����l�����Ȃ��B
�@�т́A���ٌ̈`�ŁA���� �͔������̏ی`���Ƃ���[78]�B���ɂ��ƂÂ��Ƃ��Ă��A�u�������v�Ƃ͉���
�Ӗ�����̂��낤���B�r�������ɋꂵ�ށB
�͔������̏ی`���Ƃ���[78]�B���ɂ��ƂÂ��Ƃ��Ă��A�u�������v�Ƃ͉���
�Ӗ�����̂��낤���B�r�������ɋꂵ�ށB
�@��̎w��p���Đ�����Ƃ��悤�B�Ⴆ�A�E��ŏ\�܂Ő����I������A����̎w����{�L���A�\��\���B����ŋ�\��܂Ő������邾�낤�B���� ���A��� �T �O��p���Ă��A��̎w�ł͕S��\�����Ƃ��ł��Ȃ��B�����ł���A��̎w�̎��ɓ�����v������́A���̎w�ƂȂ邾�낤�B�䂦�ɕM�҂́A�����E���[���A����� ��������M���ł���Ƃ݂�B
�@�����E���[�́A�l�ƈ�̍����ŁA����\���Ƃ���B�u��ł͐�l�P�ʂ̌R���Ȃǂ̏W���𐔂���P�ʂ��낤���B�É���ts�fen�͐i�Ɠ��ꌹ�ŁA�� �֎��� �� �i�ޑ傫�Ȑ����Ӗ�����Ƃ���[79]�B�S�𑽐��Ƃ��邽�߁A�S�ȏ�������ł���̂͌����܂ł��Ȃ��B�S���灨�݂̗��������ƁA��͕S���݂̊Ԃ��߂� �u���ւƐi�ށv���ʂƂ��đ��������B
�@�e�R�́A�Ì`�� �ł��邱�Ƃ���A�l�Ə\�Ƃ̍����Ƃ���B�l�͐����B��͏\�̕S�{�ő吔����
��A�S����Ɣ��Ƃ̍����ł���̂ɑ��A�Ƃ��ɏ\�̎���g�ݍ��킹���Ƃ���[80]�B��͂荇���ɂ��ƂÂ����A�l�ƈ�ł͂Ȃ��A�l�Ə\�̍������Ƃ����B��
���ʂɂ�������Ƃ���l���ł͂Ȃ��B�O�q�̂��Ƃ��A�u�\�v�͈�̈Ӗ���
���邽�߁A���ɓK��Ȃ��B�܂��A�M�҂̈��������ɂ́A�Ì`��
�ł��邱�Ƃ���A�l�Ə\�Ƃ̍����Ƃ���B�l�͐����B��͏\�̕S�{�ő吔����
��A�S����Ɣ��Ƃ̍����ł���̂ɑ��A�Ƃ��ɏ\�̎���g�ݍ��킹���Ƃ���[80]�B��͂荇���ɂ��ƂÂ����A�l�ƈ�ł͂Ȃ��A�l�Ə\�̍������Ƃ����B��
���ʂɂ�������Ƃ���l���ł͂Ȃ��B�O�q�̂��Ƃ��A�u�\�v�͈�̈Ӗ���
���邽�߁A���ɓK��Ȃ��B�܂��A�M�҂̈��������ɂ́A�Ì`�� �������炸�A�e�R���Q�l�ɂ������������L���Ă��Ȃ��B�e�R
���Z���������
�u�E�v�Ɣ��f�����A���邢�͋����̏\�̎��`�ł���
�������炸�A�e�R���Q�l�ɂ������������L���Ă��Ȃ��B�e�R
���Z���������
�u�E�v�Ɣ��f�����A���邢�͋����̏\�̎��`�ł���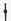 [81]�ƍ��������\�������邾�낤�B������ɂ���A�{��
�͐M�ߐ����Ȃ��B
[81]�ƍ��������\�������邾�낤�B������ɂ���A�{��
�͐M�ߐ����Ȃ��B
�@�ȏ�̐��ȊO�ɂ��A�������R�͈قȂ邪�u�l�v��u�g�v�Ɗ֘A�Â��������ł���B����́A�u�l�Ԃ̏ی`�ł���A�v�Z�̎�i�Ƃ��āw��x�ɗ��p��
�ꂽ��
�́v[82]�Ƃ���B�l�Ԃ̏ی`�𐔗ʂ̐�ɓ��Ă����R�͋L����Ă��Ȃ��B�����́A�l�Ԃ̑��ڂ̕����ɒZ����{�����{�����`�ŁA�Z���͑吔�Ƃ��Ă̋�����
�Ӗ����Ƃ���[83]�B�����������̓_����l����ƁA�{�͂�1�Ō��_�Â������Ƃ��A�Ⴆ�ΎO�炪 �̂��Ƃ��������߁A�����ł͂Ȃ���̈�
���ł���͂����B
�̂��Ƃ��������߁A�����ł͂Ȃ���̈�
���ł���͂����B
�@�܂��A�����E���[���̂��Ƃ��A���ɂ����ڂ����������B�т́A��Ɛg�̌É����߂��ƌ��āA�g�̏ȗ��`�Ƃ���[84]�B�Ղ́A��ɂ͂��Ƃ��Ɖ����� ���A�l �� �炪�����ł��邽�߁A�l����Đ�ɂ����Ƃ���[85]�B
�@�����E���[���ł́A�������Ӗ�����S�E��E�݂ɂ����āA��͊m���Ɏ����ɂȂ���|�X�g�ɂ���B���`���猩�Ă��A�l�Ɉ���������Ƃ�����B�т�� �́A�� �� �l��g�Ɖ����߂��Ƃ���������`�ɔ����Ȃ��B�l����ɓ��Ă�ꂽ�_�ɑ��ẮA�����ɂ��ƂÂ��Ƃ��铡���E���[���ƁA�ꁨ�\���S����̗���ň�т������ ���������B��̓I�ɂ́A�{�͂�6�Ŏ��グ�����B
�@���`�̓���������ƁA�\�O�����̒��ōł����G�ł���B�e�R�́A���̒��̏ی`�Ƃ���[86]�B
�@�����͂�������T�\���ɗR������Ƃ݂�B����́A�T�\���̏ی`�Ƃ���B�T�\�������̐��Ԗʂ̓��������A�����ƌ��т���B���ِ��ŗ����z������ �Ƒ��� �� �q��w�����ĕ����A���邢�͂��낼��ƏW�܂�Q�����鐫����[87]�B�����E���[�́A�T�\���������̎q���Y�ނ��Ƃ���A�����̏ے��Ƃ����B�S���ǂ�� �R������Ƃ����̂Ǝ����l�����B�Ñ�ł�miuan�Ɣ������A�Ȃ■�Ɠ��ꌹ�ŁA�������������Ӗ�����Ƃ���[88]�B
�@�T�\���̐��ԂƂ��ẮA���䂪���������̂ق��A�Ő��̋�������������B�����́A�T�\�����Q����Ȃ����Ƃ��̌̐��̑����ɉ����A�Ő����l �X�̈� �� �ɑ傢�Ȃ鋰�|�S��A�������Ƃ���[89]�B�������Ȃ��ꂽ����ɁA�����Ȃ鐶�������݂������͕s���ł���B�T�\���Ɠ��l�̓��������N���͂ǂ����B�� ���������ł���A�N�����݂̎��`�Ƃ��Ă��悢�̂ł͂Ȃ����B�������A�N���ł͂Ȃ��A�T�\�����݂Ƃ��ėp����ꂽ���R�ɑ�������Ȃ����߁A�𖾂����� ���B�������A�ȏ�̓�������A�T�\�������������l�X�ɁA���|�S�Ȃǂ̉��炩�̉e����^���鑶�݂ł������Ƃ�����B�N�����݂ɓ��ĂĂ��悢���A���`����N�� �ł͂Ȃ��T�\���ł���Ɣ��f�ł��邽�߁A�T�\���̏ی`�ł���Ƃ���B
�@�{�͂�4�Ŏ������A�����E���[���Ǝ��������̓I�ɋ����悤�B
�@�O�҂́A�S�ȏ���u�����v�̏ے��Ƃ���B�������݂���Ώۂ��A�����̐��ʂɓ��Ă�Ƃ���G�W�v�g����[90]�Ɠ������_�Ɏ���B�l�Ԃ̑̂������� �\�� �� �����鐔�ɂȂ�ƁA���������Ώۂ����߂邾�낤�B���ꂼ��̈ʂɉ��Ă邩�́A���ʂ̒��x���Ɉς˂���B�܂��A�㐢�ɕ҂܂ꂽ�����ŌÂ̎��W�ł� ��w���o�x�̗�����Ă݂�B�{���ɋL�ڂ̂��銿�������A�Ӗ������킹�ē��v�����B��͂�S�ȏ�ł́A�u�����v�̌`�e�Ƃ��Ă����p�����Ă��Ȃ�[91]�B
�@��҂́A�w�i��j�����킹�����i�\�j�����E���̎w�i�S�j���l�̑̑S�́i��j�̗���Ŕ��W�����邱�ƂɂȂ�B���n����̐l�X���A�w�Ő������������l ���� �A ���̌��_�ł������w�ɂ��ƂÂ��ƍl����̂́A���ɓK���Ă���B���̎w��{���S�������A�葫�̎w����ŕ\������Ȃ��Ȃ�ƁA�̑S�̂Ƃ��闬��ł���B���� ����̐��ɑΉ�����Ώۂ����߂Ă����l���ł���B
�@��������M���ł��錩���ł���B�������M�҂͈�̋^���������B�����ɂ���A�l�Ԃ̑̂̈ꕔ�ɂ���A�l�Ԃ̖̑сA�Ƃ��ɓ����͒��ڂ���Ȃ��̂�
�낤
���B
���������ł���ʂɒB����قǂ̑����ł���B�����̑ΏۂƂ��Ă͏[���ł���B�����A���`������Ɓu�b�v��u �v
�Ȃǂ��\������A�\��O�\�ƍ������₷���B�܂��A�����̏ی`�𐔈ʂƂ��ėp
����A��̏ꍇ�u�{�v�ƂȂ�A���i�{�j�Ƃ̍�����������Ȃ����߁A����
�Ɍ�����B
�v
�Ȃǂ��\������A�\��O�\�ƍ������₷���B�܂��A�����̏ی`�𐔈ʂƂ��ėp
����A��̏ꍇ�u�{�v�ƂȂ�A���i�{�j�Ƃ̍�����������Ȃ����߁A����
�Ɍ�����B
�@�ق��̕����ƍ�������ȏ�A�����Ƃ��Ă͋@�\���ʂ����Ȃ��B�䂦�ɍ̗p����Ȃ������̂��낤�B
�@�{�n���A�Ƃ��ɕS�ȏ�ɂ����ẮA�w�ɂ��ƂÂ��Ƃ�������A��菭�Ȃ��Ȃ�B��͂�A�����ɂ��ƂÂ��l����A��̎w���o���_�Ƃ��Đ��ʂƂȂ�Ώ� ���ق� �� ���߂�l���ɂ��A�������ꂽ�ƕM�҂͌��_�Â���B
�@�b�������ɍ��܂ꂽ���`����A�ꂩ���݂̋N�����l�@�����B��O��������̂́A�\�O�����ɂ����ėގ��_��֘A����������B�݂ɂ͊Y�����Ȃ����A�� �{�I�� �� �搔���ꂩ��l��Ɏ��܂�ȑf�Ȏ��`�Ƃ���_�ł���B�����͓��Е����ɂ��p�������A�g�p�p�x�̍���������������B����䂦�A�ɎG�ȕ����͗����Ɍ������ ���āA�����ɂ͗p�����Ȃ��ƍl������B�܂���Ϗ��������_�́A��˂ł̔F���ɍ������v�������邪�A�ɎG���������Ӑ}������A���t���ƂȂ�B�搔 �̑����݂́A�����Ƃ��Ă̎g�p�p�x������߂ĒႢ���ߕs�s���������Ȃ��Ƃ����悤�B
�@���āA�ꂩ���݂̋N�����܂Ƃ߂����B�����̌��_����ꂪ�A�d�v�Ȗ��ƂȂ�B�u�b�v�ŋL�����\�Ƃ̊W������A���`�Ƃ��ẮA�ق��̕����Ƃ̍� ������� ��K�v������B�M�҂́A���Е����ɂ������Ə\�̋�ʂ̖��������ł��Ȃ������B�������b�������ł́A�㉺����܂邽�߁A���ꂼ��̊������������Ȃ镶�� �ł��邩�A�������Ƃ͂Ȃ��Ȃ����B
�@�ꂩ��l�܂ł́A���ׂĐϏ��\�L�����B�w��Z�Ԃ̏ی`����邩�ۂ��Ɋւ�炸�A�܂���ӂł���Ƃ��Ă��A��������w�������ƂɂȂ�Ƃ�����B �M�� �́A ���̔z�u�Ⓑ�Z�ɈӖ�������ƍl�������A�K�����������������A��ӂƂ͍l���������Ƃ���B�������Ϗ��ł��邽�߁A��̗ݐρA�܂��{��{��{��̂��Ƃ� ��ӂł���\���͔ے�ł��Ȃ��B
�@�܂����܂łɂ����Ă��A�ȑf�Ȏ��`���O��ƂȂ�B����ɐ��ʂ̐�߂�|�X�g��A�����̂��C���[�W�����`�̍\���v�f�ƂȂ�B
�@�\�͎��`����@����ɁA��T�O�ɂ�肤�܂��A�ŏ��̈ʂ�\�����ł��邽�߁A���P�ɏc�ɂ��������ƍl���Ă悢�B�S�A��A�݂́A���ڂ���Ȃ����� �̖т� �����A�l�Ԃ��̂ɔ�������̐����͂邩�ɒ��z���鐔�ʂł���B����đ����̃C���[�W�������`�ɁA��Ƃ��ĒP����t�����`�ł���Ƃ�����B
�@�{�e�ł́A�w�ɂ�鐔������A���n����̐l�X�̐��ɑ��鐳�m�ȔF���\�͂��𖾂����Ȃ������B�܂�܈ȏ�ɂ����āA���`���w�ɂ�鐔�����ɗR�� ����� �\ ���͔ے�ł��Ȃ��B�������������������ł̍l�@���A����̉ۑ�ƂȂ�B�܂��A�b�������Ȍ�̋�����⽕��A�ꏑ�Ȃǂ̎��`������Ȃ����߁A���`�̕ϑJ�� �܂��������ł̍l�@���A�N�����𖾂����|����ƂȂ肤�邾�낤�B
[1]�����ŌÂ̕����͍b�������Ƃ���Ă����B�����A2005�N10��07���ɍX�V���ꂽhttp: //headlines.yahoo.co.jp./hl?a=20051006-00000414-yom-soci�̋L���͈ȉ��̂��Ƃ��`����B�V�� �ВʐM��2005�N10��5���A�u��̍b��������萔��N�O�̊G�����������������ꂽ�ƕ���B��C�ÐЏo�ŎЂ̌Õ������ƁA���i�_�̊Ӓ�̌��ʁA �u�����j���������̉\������v�Ƃ̌��_�Ɏ���B�����������_�ł́A�قƂ�ǂ�����ǂ��Ƃ����B����āA����m���w�Ñ㒆���l�́u���ϔO�v�F�b�������̉� �w�I�l�@�𒆐S�Ƃ��āx�A141�łɋL����邲�Ƃ��A�u���������̌��n�`�����߁A���̍\���̗��_�I��͂����݂�ɓ������ẮA�b��������ΏۂƂ��čs���� �قڌ��Ȃ��v�Ƃ��čl�@��i�߂����B
[2]���������w�i�����E�����u�b�N�X�j��������\���������l�Ԃ̕����x�A8-9�łɂ́A�ȉ��̂��Ƃ��L����Ă���B�u�����̐��藧����������� ������ ���āA���ݎ����������邱�Ƃ̂ł���ŌÂ̎����́A�㊿����iA.D.25~220�j�̊w�ҋ��T�̒������w���������x�i�����āw�����x�Ƃ������j�ł� ��B�c���T�͓��R�̂��Ƃł͂��邪�b�������͌��Ă��炸�A⽕��𒆐S�ɉ�����Ă���̂ŁA���Ɍ�����������Ȃ��ł͂Ȃ����A�����̐��藧�����l������ �́A�w�����x�������ɕ����������Ƃ͂ł��Ȃ��v�ƁB�����A���T�̐��͎v�z���������A���Ȍᒘ�w�b�������ߗсx�A96-97�łɁu�������߈ꎚ�A��L�_�� ���A�����{�`�B�Z�������Ȏw���ی`��A�A���n�w������^��O�l�Ϗ��V�o���A�����昰�ی`���A�ȑ��ȕֈՈז�B���ސϏ����A�{���C���_�鐫�V���v�� ����B�܂��w�Õ����e�сx10���A885�Łi���F��w�b�������W�ߑ�\�l�x�j�́A�Z�̎����������ɓ�����A�u�����B�w�Z�B�ՔV���B�A�ω��Z�B�������B�] ���B�]���B�x�Z���搬�B�Ռo�ӏo�B�����V�w�����v�Ƃ���B�Ղ͘Z�̑�������ɂł������߁A���T�̐����U��ł���Ƃ���̂��B�b�������ɂ͊W���Ȃ��Ƃ� ����B����āw�����x����сw�����x���݂̐��A����ɉA�z�܍s��Ղɂ��ƂÂ����́A�����Ƃ��Ĉ���Ȃ��B
[3]�w�b�����ҁx�ɋL�ڂ̂���b�������̎��`��蔻�f����B��̈ʂɑ����A��{�I�ɉ����݂̂ŕ\�L����鐔���i�n���`�j�B��̈ʂɑ����A��{�I�� �Ϗ��� �����ĕ\�L����鐔���i�n���a�j�B�\�̈ʈȏ�̈ʂ�\���P�ʂƂȂ鐔���i�n���b�j�B
[4]�W�����W���E�C�t���[�w�����̗��j�F�l�ނ͐����ǂ̂悤�ɂ������Ă������x�A2-35�ŁB
[5]�h�D�j�E�Q�[�W�w���̗��j�x�A19-37�ŁB�O�f����[4]�A110-115�ŁB
[6]�s����w�b�����������x�A115�łɁA�u��������B�Õ����O�l������O亖�A����w�V�ی`��v�Ƃ���B�����w���������x�A2�ł����l�ɐ��� ����B
[7]�O�f����[4]�A28�ŁB
[8]�O�f����[4]�A96�ŁB
[9]�����w�����`�`�w�T�_�x�A221�łɁA�u��A����A�ێZ�Ԉꖇ���z�V�`�B�o�Õ��o�A�����ӎ������v�Ƃ���B
[10]�e�R�C�w�����N���̌����x�A51�ŁB�w�Õ����e�сx1���A7�Łi���F��w�b�������W�ߑ��x�j�����l�ɐ�������B
[11]�O�f����[4]�A28�ŁB
[12]����m�w�Ñ㒆���l�́u���ϔO�v�F�b�������̉Ȋw�I�l�@�𒆐S�Ƃ��āx�A239-240�ŁB�܂��O�f����[10]�A60�ł����l�ɐ����� ��B
[13]�O�f����[10]�A59�ł́u�O�̎��̌Â��`�̂��̂ɂ� �̂��Ƃ��Ȃ��Ă�����̂����邪�A�����
�M���ɂ������Ă̏K����̂��̂ƌ��Ă��������͂Ȃ��낤�v�Ƃ���B�B��A�Â����`�������ďq�ׂ������B�����A�{
���ɂ͍������L����Ă��炸�A�m�肵�������B�܂������A440�ł́A�������́u���ׂāw�ی`�x���w�w���x�łȂ���Ȃ�Ȃ��v�Ƃ���B���������҂́A����
�ɂ�������ׂ̍����z�u�ɂ͒��ڂ��Ă��Ȃ��B����ĕM�҂́A���̔z�u�̍l�@���s�킸�ɖ{�����m��ł��Ȃ��B���̔z�u�ɁA�Ӗ�������\��������Ř_�q����
���B
�̂��Ƃ��Ȃ��Ă�����̂����邪�A�����
�M���ɂ������Ă̏K����̂��̂ƌ��Ă��������͂Ȃ��낤�v�Ƃ���B�B��A�Â����`�������ďq�ׂ������B�����A�{
���ɂ͍������L����Ă��炸�A�m�肵�������B�܂������A440�ł́A�������́u���ׂāw�ی`�x���w�w���x�łȂ���Ȃ�Ȃ��v�Ƃ���B���������҂́A����
�ɂ�������ׂ̍����z�u�ɂ͒��ڂ��Ă��Ȃ��B����ĕM�҂́A���̔z�u�̍l�@���s�킸�ɖ{�����m��ł��Ȃ��B���̔z�u�ɁA�Ӗ�������\��������Ř_�q����
���B
[14]���͂ň������`�́w�b�����ҁx��515�Łi��j�A14�Łi�O�j�A538�Łi�l�j���]�ڂ���B�������A�}3�i�E�j�͑O�f����[10]��� �]�ڂ� ��B
[15]�O�f����[10]�A51-52�ŁB
[16]�O�f����[12]�A208�ŁB
[17]�Õ����e�ѕҎ[�ψ���w�Õ����e�сx1���A2�Łi���g���w��������x�j�́A�u�`�w�V�n�A�R���_���������A�̌Õ����ꎊ亖�A���ȐϏ����`�v�� ����B
[18]�O�f����[6]�A115�łɁu��w���ȉ����H�H�A���Ȏ�쐔�A�����S�V�ԕK��o�E���A�|���d�w��A�c�B���O�l�ϓ|�w�A�̉�����v�Ƃ� ��B
[19]�O�f����[14]�A540�ŁB
[20]�O�f����[4]�A31�ł́A���̗v�f�ł����Ə������A�ȉ��̂��Ƃ���`����B��Ƃ́A�u���߂ɒP�ʈ��\�����̂Ƃ��Č���ƂȂ�ے� �L���� ���߂āA���̒P�ʂ���Ƃ��鐔�Ɠ�������������J��Ԃ��v���Ƃł���B���鏘���Ƃ́A�u�ꂩ��n�܂鑊���������ɁA�݂��ɉ��̊W���Ȃ��ʌ̏ے��L ����^����v���ƂƂ���B�l�����w���珬�w�ւƏ��ԂɎw���o���s�ׂ́A�{���A��i�l�����w�j�A��{��i���w�j�A��{��{��i��w�j�A��{��{��{��i�� �w�j�̍l���ł���A��̊T�O�ɏ]���B
[21]�O�f����[10]�A56�ŁB
[22]�������ہE���[����w�w������W�����a���T�x�A893�ł́A���`�̔������d�������̂�⽕�����ŁA�b���E�����͊W�Ȃ��Ƃ���B����āA ������ �ړI�Ƃ��������̒��Z�̒��߂́A�b�������ɂ͂Ȃ����ƂɂȂ�B
[23]�O�f����[10]�A58�ŁB���`������A�}3�i�E�j�ɂȂ邾�낤�B�������e�R�́A���`���u�O�̎��̌Â��`�v�Ƃ������ŁA���Ƃɂ����� ������ �L�ڂ��Ȃ��B
[24]�O�f����[4]�A12�ŁB�C�t���[�́A�I�[�X�g�����A�̃A�����_�������������̂Ƃ��ē�ꂵ���m��Ȃ�����������グ��B�ނ�̌���� �́A��� �\��ninta�ƁA��\��tara�ɂ��ƂÂ��Ƃ����B�O��tara-mi-ninta�i��ƈ�j�A�l��tara-ma-tara�i��Ɠ�j�ƌ��������� ���B�Ȃ������͎̂l�Ŏ~�܂�A�l����̐��́u��������v���Ӗ����錾�t��p�����Ƃ����B�}���[�����̈ꕔ�̌��Z�������A�g���X�C���̐����ɏZ�ޕ������� �l�̎�@���̗p���邻�����B�{�łɂ́A��������p����v����̖������Љ��Ă���B
[25]�O�f����[4]�A31�ł́A��Ə����̂����ꂩ�̌��������Ƃɂ��āA�l�ނ͂�������̐���\������@�������Ƃ���B
[26]�O�f����[17]�A10���A853�Łi���c�����w���ؕя\��x�j�Ɂu亖�������`��v�Ƃ���B
[27]�O�f����[10]�A60-67�ŁB
[28]�����w���������x�A6-10�ŁB
[29]�O�f����[22]�A30�Łi�܁j�A80�Łi�Z�j�A5�Łi���j�A78�Łi���j�A23�Łi��j�B�������ہw�����ꌹ���T�x�i���Łj��1967 �N�A�O �f����[22]��2001�N�o�łł���B�O�҂͘Z�̋L�q���ڂ����A�܂����҂̐��ɂ͕\����Ŏ�̑��Ⴊ���邽�߁A���̏ꍇ�͂��V������҂̌����ɏ] ���B
[30]�O�f����[10]�́A�Z�i64�ŁA��ܐ}�j�Ɣ��i66�ŁA�攪�}�j�̎�܂˂��ڂ���B
�i�Z�j �@�i���j
�@�i���j
[31]�O�f����[12]�A212-215�ŁB
[32]�O�f����[12]�A154�ł́A�u�������w�i�}�}�A���j�ɂ����ẮA�܂܂łŁA�Ƃɂ������肪���Ă���킯�ł��邩��A���ꂪ�ʂ��� �č��E �ǂ���̎���ۂ��Ă���̂��v�ƁA�Ў�Ő��������Ƃ�O��ɁA������̖��̋c�_��i�߂Ă���B�u���Ƃ��Η�����ɕ���������Ă���Ƃ���ƁA���\���͗� ����łȂ����̎�ɂȂ�v���߁A�Ў�Ő����邱�ƂɂȂ�B
[33]���\���Ɗs�������܂˂𐔂ɓ��Ă��Ƃ��邪�A�܂����̂��ׂĂɂ����Ă͓��ꂳ��Ă��Ȃ��B
[34]�O�f����[12]�A436�ł́A���������̌o�H���A�u���t�i�����j���g�U����U�聨�������ꁨ�����v�̗���ł���Ƃ���B
[35]�O�f����[22]�A30�ŁB
[36]��猁w�������w�ʎj�E��Ó��ܑ㊪�x�A43�ł��L�ڂ���O��̖��@�w�B�v�Z���Ȃ���邽�ߑ����ɂ͊W�Ȃ����A���ʂƂ��āA�܂������Ɉʒu ����_ �𖾂炩�ɂ��鎑���ł���B
[37]�O�f����[17]�A10���A879�Łi�k���B�w�����`�`�w�x�j�́A�u�~���ߔV�ߔV�{���A������ߎҁA�߁~������ؖ�v�Ƃ���B
[38]�O�f�����A30�ŁB
[39]�b���ȑO�ɂ́A���Е���������B�O�f����[12]�A114�ł́A�u���Е����́A�v����ɐ�������������������Ă��Ȃ��B������Ƃ����āA�� ���� �w���������l�Ă���Ă��Ȃ������x�ƒf�肷�邱�Ƃ͑��v�ł��낤�B�������A���ɁA���̂悤�ȌÂ�����Ɋ��ɐ������g�p����Ă����Ƃ��������́A�f���ɔF �߂Ȃ���Ȃ�܂��v�Ƃ���B���ǁA�����̑��݂͍b���ȑO�Ɍ����邪�A�߂��܂���ɑ������ꂽ�Ƃ������Ȃ��B���݂ɑO�f����[36]�A30�łɂ�� �A���Е����̌܂́~�ł���B
[40]�O�f����[17]�A10���A877�Łi���\�v�w�Ԉ��V�R��l�ߊ��\���x�j�́A�u �i���b�]���j�Õ��܁v�Ƃ���B
�i���b�]���j�Õ��܁v�Ƃ���B
[41]�O�f����[12]�A241�łɎ��������ł́A�O�f����[17]�A10���A877�Łi�����w�Õ����ω����x�j���A�u亖�߈ɐ��A�������@��
������
���A�^亖���Ս��A���s�֏��A�T��亖�V�������V�`�A���㉺�s�ρA�� ��
���v�Ƃ���B�܂�Ϗ��ɂ����亖�ƍ������₷���A�����̂ɕs�ւł��邽�߁A���̓�{���~�ɕό`���A�㉺�̐��ƌ��������������B
��
���v�Ƃ���B�܂�Ϗ��ɂ����亖�ƍ������₷���A�����̂ɕs�ւł��邽�߁A���̓�{���~�ɕό`���A�㉺�̐��ƌ��������������B
[42]�O�f����[36]�A32�łɁu�L�������e�Ս����A�@�w�\�x�^�w�b�x�A�w �x�^�w
�x�^�w �x�A
�w
�x�A
�w �x�^�w
�x�^�w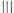 �x�A�w�~�x�^�w�{�x�A�K�{�m������
�w���x�I���˔\�m����哪�����A�@�ʔc����
���ʓƗ����݈�s�m�㉺�I�n���A���\�i�s�ȑz�A�����@�y�m�����B�c�w�~�x�I
��A���e���ꉡ�控���A���ׁw�܁x�A���s�^�w�{�x�����v�Ƃ���B�������A���Е����ɂ������i�\�j�Ə\�i�b�j�̍���������������@�͏q�ׂ��Ă��Ȃ��B
�x�A�w�~�x�^�w�{�x�A�K�{�m������
�w���x�I���˔\�m����哪�����A�@�ʔc����
���ʓƗ����݈�s�m�㉺�I�n���A���\�i�s�ȑz�A�����@�y�m�����B�c�w�~�x�I
��A���e���ꉡ�控���A���ׁw�܁x�A���s�^�w�{�x�����v�Ƃ���B�������A���Е����ɂ������i�\�j�Ə\�i�b�j�̍���������������@�͏q�ׂ��Ă��Ȃ��B
[43]�O�f����[22]�A80�ŁB
[44]�O�f����[17]�A10���A884�Łi���R�w�����Ëb�F���j�ꌾ�������W����{�ꕪ�x�j�́A�u�ÊF�ؓ��טZ���߁v�Ƃ���B�����A885�� �i���F�� �w�b�������W�ߑ�\�l�x�j�����l�ɐ�������B
[45]���Ȍ�w�b�������ߗсx�A98�ł́A�u �טZ�V�����B�b�����Z����
�טZ�V�����B�b�����Z���� �ҁA�T�����m�������V�I�����B�c�������p���m���V���ҁA����
�ҁA�T�����m�������V�I�����B�c�������p���m���V���ҁA����
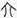
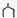
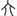 ���`�B���s��
���`�B���s�� �A�ȑ��^�����`���Ս��v�Ƃ���B
�A�ȑ��^�����`���Ս��v�Ƃ���B
[46]�O�f����[17]�A10���A885�Łi���\���w�b�����������I�u���v�F���j�ꌾ�������W����l�\�Z���x�j�́A�u�ݍb�������A�w�Z�x���L����
�w �x�A�����^�w���x���v�L���ʁB�c�ޑ��݁w���x�^�w�Z�x���������m�����I
�����s�����v�Ƃ���B
�x�A�����^�w���x���v�L���ʁB�c�ޑ��݁w���x�^�w�Z�x���������m�����I
�����s�����v�Ƃ���B
[47]�O�f����[22]�A5�ŁB�܂��������ہw�����ꌹ�����x�A777�ł́A�u���i�g�ݕ����j�ł����A�O�{�O�{��̂悤�ɁA�s����Ȓ[���� ���v�� ����B
[48]�O�f����[12]�A214�229�ŁB�{������������A���@�����݂��Ȃ����낤�B�Z�p�̉����揜�i�l���j�ɂ����āA���@�ƌ��@�A��@�Ə� �@���A ���ꂼ��Ή�����B�������̉������߂�ߒ��ŁA�E�ӂƍ��ӂňڍ�����ۂɁ{����|�A�~���灀�i�t�����l�j�ƕϊ����邱�Ƃ�������f�ł���B
[49]�O�f����[17]�A10���A887�Łi�ы`���w�������O�x�j�́A�u�Í�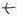 �i���E�����j�B�����ؔV�Õ��v�Ƃ���B��
���A888�Łi���R�w�����Ëb�F���j�ꌾ�������W����{�ꕪ�x�j���A�u�{�{�ۓ����ؒf�`�A���؈����ꖼ�v�ƁA��
������Ƃ��̌`�Ƃ݂�B��Ď��̐����Ƃ����Ƃ���B
�i���E�����j�B�����ؔV�Õ��v�Ƃ���B��
���A888�Łi���R�w�����Ëb�F���j�ꌾ�������W����{�ꕪ�x�j���A�u�{�{�ۓ����ؒf�`�A���؈����ꖼ�v�ƁA��
������Ƃ��̌`�Ƃ݂�B��Ď��̐����Ƃ����Ƃ���B
[50]�O�f����[22]�A78�ŁB
[51]�O�f����[17]�A1���A622�Łi�����u�w��������O�сx�j�́A�u���V�{�ӈו��B���ە��w�V�`�B�w�����v�Ƃ���B�����A623�Łi���� ���w�b �������T����x�j���A�u�b�����T�ȓ��w�A�������J�A�ȕ\�����ʔV�`�B�m�����ؗp�I���V���v�Ƃ���B�����ė����ɊJ���`�Łu���ʁv�̈Ӗ���\�� ���A��Đ����ɂ����Ƃ����B
[52]�O�f����[17]�A1���A623�Łi���\���w�b�����������I�u���v�F���j�ꌾ�������W����l�\�Z�{�x�j�́A�u���ʑ��w�_����풊�ۓI�ӔO�A ���`�� �ہB�����A�������\�Z���w�����ۈӎ��B�c�ߖ������I�N���A���^��̕��ۗL�ցA���\���ۗ��]�ΐL�V�`�A���Ґ��ە��L�d�w�^�H�w�V�`�v�Ƃ���B
[53]�O�f����[17]�A1���A622�Łi�n���ρw���������Z���a�؊��O�x�j�́A�u�����]�V�����B�c�]���������R�B�ޑ����B���]���z���g�V�� �ӁB�̖� �����ʎ����B���؈ו��ʔV���B�̖��ו��ʔV�����v�Ƃ���B
[54]�O�f����[22]�A158�ŁB
[55]�O�f����[17]�A10���A894�Łi�ы`���w�������O�x�j�́A�u�{�`���ȁB��ؗp�א����B�̋��ȔV�`�ʈȑ����הV�v�Ƃ���B
[56]�O�f����[17]�A10���A895�Łi���R�w�����Ëb�F���j�ꌾ�������W����{�ꕪ�x�j�́A�u��{�I���A���]�ߌ`�A�������丩���A�A�] �߉� �L�A���L�����Ӂv�Ƃ���B�����A895�Łi���`�m�w�����������b�������l�߁x�j�́A�u�ێ�y�]�ߌ`�A���I�V�{���A��א����v�Ƃ���B���r�̐߂̌`�ŁA �I�̖{���̎��ŁA��Đ����̋�Ƃ����̂��Ƃ����B
[57]�O�f����[17]�A10���A895�Łi�n���ρw���������Z���a�؊���\�Z�x�j�́A�u�I�V�����B�]���ی`�B�w����v�Ƃ���B
[58]�O�f����[17]�A10���A895-896�Łi���F��w�b�������W�ߑ�\�l�x�j�́A�u�_������ �B�Ԗ���
�B�Ԗ��� �B�O���^
�B�O���^ �i���j���B���������i���]�`�j�����ȔV�Ȏ��I�V���݁B�����������B��叚�I�V
�ی`���Ȉא����V��B���s���s另���`���V�I�ȑ�V�B�I���ÊW��肍�B�ȋ�^����
���^���ʁv�Ƃ���B
�i���j���B���������i���]�`�j�����ȔV�Ȏ��I�V���݁B�����������B��叚�I�V
�ی`���Ȉא����V��B���s���s另���`���V�I�ȑ�V�B�I���ÊW��肍�B�ȋ�^����
���^���ʁv�Ƃ���B
[59]�O�f����[17]�A10���A894-895�Łi���c�����w���ؕјZ�x�j�́A�u�}�n��L�ꎚ�B�����ד�B�����O�B������亖�B���ψ�� �\�B�� �\�ׁ~�B�ρ~�ה��B����Z�]�����B�����\����v�Ƃ���B
[60]�O�f����[17]�A10���A883�Łi���g���w��������x�j�́A�w�����x�́u�Z�v�̐��������āA���̂��Ƃ���������B�����A���Łi���T�w�� ���x�j �́A�u�]���B�]���v�Ƃ��A�����Z����ɑ��݂��邱�ƂɂȂ�B�������A���́u���ˋ����A������������L�����A���㍇���Ȑ��Z�A�������L��ʁv�ƁA��ɔ��� ����A��ɓ��Ɣ������킹�ĘZ�Ƃ���̂́A�����ɍ���Ȃ��Ƃ���B
[61]�O�f����[45]�A97�ł́A�u�ώ��l���ߊo���ɁB���s���s���ɈȁA�������ȁ~�הV�v�Ƃ���B����̕��G��������邽�߂ɁA�Ϗ���p�� �Ȃ��� �����B�m���ɁA�܂����̎��`�́A���ꂼ���l�{�̒����Ȃ����Ȑ��ō\������Ă���B�����Ƃ��̎�Ԃ͏Ȃ���Ă���Ƃ�����B
[62]�O�f����[14]�A165�Łi�S�j�A95�Łi��j�A544�Łi�݁j�B
[63]�O�f����[17]�A10���A912�Łi���\���w�b�����������I���F���j�ꌾ�������W���l�\�Z�{�O���x�j�́A�u�����I�w�݁x���A嫕s�����A�A �l�n�� �I�w�݁x����q�ȕs�Z�����B��ғI���ʁA���ݎ��`���L���\�����ړI�߈ꉡ���B����b���A�I���I�w�݁x���A�ݎ��̓I�����������ꉡ�G���l�n���I�w�݁x���A�� �v�L�߈ꉡ�v�Ƃ���B
[64]�O�f����[10]�A68�ŁB
[65]�O�f����[45]�A100�łɁu�����\������A�A���ߐi�ʁA�����^�ꍬ�A�̒����V�B���\�^��V���`�A�����c���V�ʁA�A�R���������ȏ\�i �ʁA�� �ז����v�Ƃ���B�O�f����[17]�A2���A694�Łi�������w�b�������T���O�x�j���u�b�Ñ�V�Z�ԁA�G�����ԕ\�����ʏ\�A�ȗ^�����V�Z�Ԉ��ʁv�Ƃ� ��B��Ə\��\���Ƃ��́A�Z�Ԃ̎g�p�@�̈Ⴂ�ɂ��Ƃ����B
[66]�O�f����[17]�A2���A692�Łi�n���ρw���������Z���a�؊��܁x�j�́A�u���n�ȋ��w�L���B譣�V�����B���������Z�B���Ոȑ���B�y���\ ��B���� �\�����V�d�w�B���b�V���B�P��V�ێ�w�`�B�҈���w�B�̉��V�B���ꎚ���B�b�א\�w�B�̒G�V�v�Ƃ���B
[67]�O�f����[12]�A247�ŁB
[68]�O�f����[17]�A2���A694�Łi���\���w�b�����������I�u���v�F���j�ꌾ�������W����l�\�Z�{�x�j�n���u��F�ꏶ�I�ی`�A�\�܁A ���s�� �\�A�w�\�x�����ۓI�A�\�����w�����G�V�`�A�I��w���ڈ\�A�����G���v�Ƃ���B
[69]�O�f����[22]�A115�ŁB
[70]�������ہw�����ꌹ���T�x�A797�ł́u�w�\�{�܂��͎Z�؏\�{����ɂ܂Ƃ܂����P�ʁv�Ƃ���B�������O�f����[12]�A235�łɂ�� �ƁA�Z�� �\�{���ЂƂ܂Ƃ߂ɂ��邱�ƂɈӖ��͂Ȃ��������B
[71]�O�f����[36]�A34-35�łɂ́A�����̐V�Ί펞�㖖���̐����n��\���ڂ����Ă���B�{�\�ɂ́A�\�܂ł̕\�L�@������B
[72]�O�f����[22]�A541�ŁB�O�f����[17]�A4���A43�Łi�n���ρw���������Z���a�؊����x�j���A�u�S�T�ꔒ�V�������B���Ȉא����v �ƁA���� �����ł���B
[73]�O�f����[10]�A200�ŁB
[74]�O�f����[12]�A250�ŁB
[75]�O�f����[17]�A4���A43�Łi���\���w�b�����������I���F���j�ꌾ�������W����l�\�Z�{��O���x�j�́A�u�w�S�x�����]�I�w���x�i�� ���j�A���� �@�I�ی`���A�ߖ��w�S�x���I�N���A���ۈȎw�w�@�V�`�v�Ƃ���B
[76]�O�f����[17]�A4���A42�Łi�M���w�u�_�x�j�́A�u�m��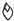
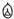
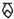 �یn�݊L�`�A
�یn�݊L�`�A �ۊL���i�q�E�A���]���S�����A����
�V���וS��B��S���S�A�^�������\
��A���ד���v�Ƃ���B
�ۊL���i�q�E�A���]���S�����A����
�V���וS��B��S���S�A�^�������\
��A���ד���v�Ƃ���B
[77]�O�f����[17]�A4���A43�Łi���j�]�w���������^�F�Êw�p����l���x�j�́A�u�����K�ܔV�`�B�Ðl��ȏ\�\�V�����B���Ȉ�ܐ��V�B�̒薼 �וS�v �Ƃ���B
[78]�O�f����[17]�A4���A42�Łi�ы`���w�������O�x�j�́A�u���ה��V���́B
 �F�۔������N�`�v�Ƃ���B
�F�۔������N�`�v�Ƃ���B
[79]�O�f����[22]�A117�ŁB
[80]�O�f����[10]�A216�ŁB
[81]�O�f����[45]�A100�ł́A�u�b�����\����b�A��������� �A
�A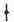 �A
�A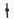 �A
�A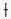 ���`�v�Ƃ���B
���`�v�Ƃ���B
[82]�O�f����[12]�A250�ŁB
[83]�O�f����[28]�A13�łɁA�u�b�����I�w��x���A�T���ݑ����l�`�I�ڏ����Z��A�ȏ��ڏ�I���ї������w��x�V���v�Ƃ���B
[84]�O�f����[17]�A2���A698�Łi�ы`���w��������x�j�́A�u��g�É��߁B�����g�V�Ȍ`�v�Ƃ���B
[85]�O�f����[17]�A2���A698�Łi�ՉƏˁw�ߐ�F���w�_�p��ꊪ��l���x�j�́A�u�R�� ���ʉ��`��B�Ȑ��ސ��V�B���א玚�V��B
�{�������B�ː���������B�l��ʘ�K
�����B�n����l�א�v�Ƃ���B����ɁA�����A699�Łi���Ȍ�w�b����������
�I���F���j�ꌾ�������W����l�\�Z�x�j���A�u�玚�I�����{�`�W�ݐl���I�������������A��w�����I�W�u�A�ȕʉ��l�A�������l���Ȉא��i�l��d�C�j�v��
����B
���ʉ��`��B�Ȑ��ސ��V�B���א玚�V��B
�{�������B�ː���������B�l��ʘ�K
�����B�n����l�א�v�Ƃ���B����ɁA�����A699�Łi���Ȍ�w�b����������
�I���F���j�ꌾ�������W����l�\�Z�x�j���A�u�玚�I�����{�`�W�ݐl���I�������������A��w�����I�W�u�A�ȕʉ��l�A�������l���Ȉא��i�l��d�C�j�v��
����B
[86]�O�f����[10]�A216�ŁB
[87]�O�f����[12]�A251�ŁB
[88]�O�f����[22]�A11�ŁB
[89]�O�f����[28]�A15�łɁu��T�����R������ʓI�Q�ځA���㎿�i�Ő����l�Y�����䐫�֑�j�I��p�v�Ƃ���B
[90]���^��E�Ж�P��Y�w��b���w�I��18�F�����Ɛ��w�L���̗��j�x�A12�ł́A��ʈȏ�̃G�W�v�g�����̋N�����A�ȉ��̂��Ƃ���������B
�i���j �@�i��j
�@�i��j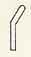 �@�i�́j
�@�i�́j �@�i�Ɂj
�@�i�Ɂj �@�i�فj
�@�i�فj
[91]���[�����w���o�x�i��j�i���j�����ƂɁA���v���Ƃ�ȉ��̕\�ɂ܂Ƃ߂��B�Ȃ��A�Q�l�ł͏ȗ�����B
| �� ���� | �� �� | ��
�� | �� �� | �� ���̗p��Ɛ� |
| �� | 33 | 7 | 26 | ����(1)�A �Ђ�����(2)�A�킸����(10)�A���(3)�A�Е� (8)�A�B��(2) |
| �� | 18 | 10 | 8 | �s��� (2)�A��(6) |
| �O | 46 | 25 | 21 | ���� (18)�A����(1)�A�s���(2) |
| �l | 93 | 46 | 47 | ����(1)�A ���́E�l��(46) |
| �� | 12 | 11 | 1 | ����(1) |
| �Z | 22 | 21 | 1 | ����(1) |
| �� | 14 | 8 | 6 | ����(4)�A ���x��(2) |
| �� | 12 | 11 | 1 | ����(1) |
| �� | 14 | 6 | 8 | ����(6)�A ���[��(2) |
| �\ | 17 | 8 | 9 | ����(7)�A ������(2) |
| �S | 70 | 0 | 70 | �����E����� ��(70) |
| �� | 12 | 0 | 12 | ���m�ꂸ�E�� ��(12) |
| �� | 47 | 0 | 47 | �ɂ߂đ����E ����(47) |
| ��
�v | 410 | 153 | 257 | |
��Q�l����
���Ȍ�w�b�������ߗсx�A���؏��ǁA�k���A1979�B
���^��E�Ж�P��Y�w��b���w�I��18�F�����Ɛ��w�L���̗��j�x�A�։ؖ[�A�����A1979�B
�s����w�b�����������x�A�Ȋw�o�ŎЁA�k���A1982�B
�e�R�C�w�����N���̌����x�A�e���Z���ЁA�����A1941�B
���������w�i�����E�����u�b�N�X�j��������\���������l�Ԃ̕����x�A�������@�A�����A2000�B
���[�����w���o�x�i��j�i���j�A�w�K�����ЁA�����A1982-1983�B
���T��A�i�ʍْ��w�����������x�A��C�ÐЏo�ŎЁA��C�A1988�B
�����w�����`�`�w�T�_�x�A�ĘD���ЁA�ϓ�A1981�B
�w�b�����ҁx�A���؏��ǁA�k���A1982�B
�Õ����e�ѕҎ[�ψ���w�Õ����e�сx�A��C����o�ŎЁA��C�A1999�B
����m�w�Ñ㒆���l�́u���ϔO�v�F�b�������̉Ȋw�I�l�@�𒆐S�Ƃ��āx�A�����o�ŁA�����A1981�B
�W�����W���E�C�t���[�w�����̗��j�F�l�ނ͐����ǂ̂悤�ɂ������Ă������x�A���}�ЁA�����A1988�B
�����w���������x�A���C�o�ŎЁA�����A2003�B
�������ہw�����ꌹ�����x�A�w���ЁA�����A1965�B
�������ہE���[����w�w������W�����a���T�x�A�w�K�����ЁA�����A2001�B
�h�D�j�E�Q�[�W�w���̗��j�x�A�n���ЁA���A1998�B
��猁w�������w�ʎj�E��Ó��ܑ㊪�x�A�]�h����o�ŎЁA�싞�A1997�B
�i�O-^�j���٘_���쐬����ɓ�����A���w������т��x���������������[��������A�^������ ���A����R��q�������ɐ[�Ӑ\���グ��B�ȏ�������Ė{�e���I������B