身体重心

つり合いで求める人の重心位置

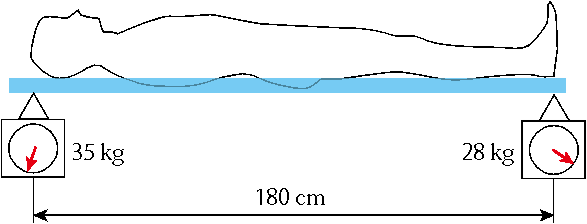
人の重心を考える時も、「重心はつり合い点だ」ということは変わりません。立位の人をそのままの状態で寝かせた時を想像して下さい。ここでは、身長１８０㎝の人を想定してます。頭頂と足底に合わせた位置にその点の荷重が測れるようにしてあります。体重計の計測値から、つり合い点である重心位置を求めます。

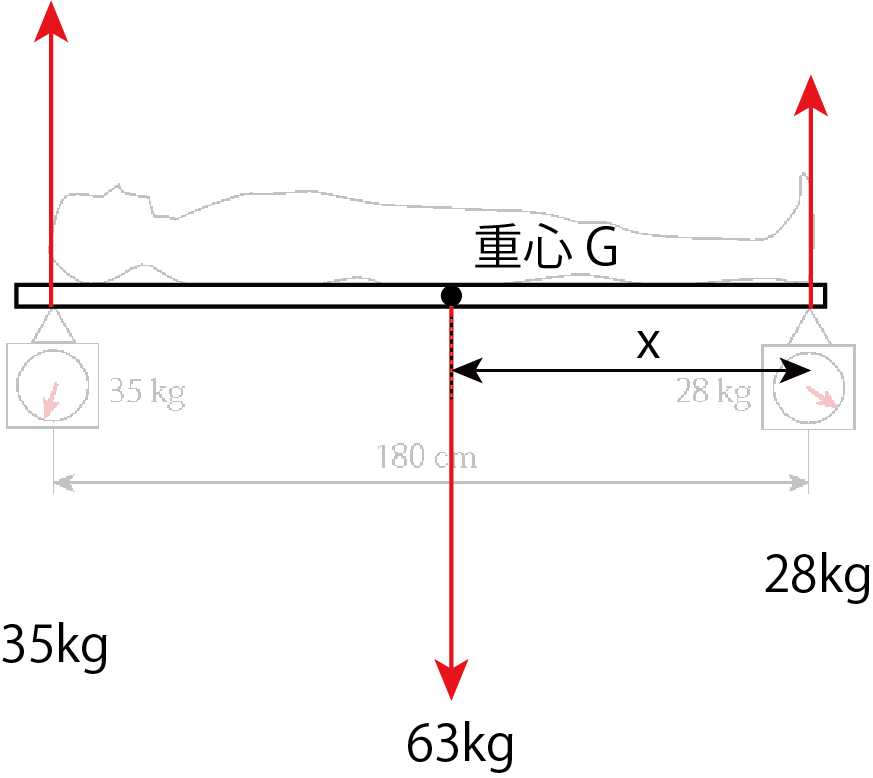
足の荷重点から重心Gまでの距離をｘとします。このベッドは回転せず、水平を保っていますので、モーメント（回転力）はゼロです。今、時計回りの方向のモーメントを＋とすると、このベッドの足底の荷重点まわりのつり合い式は。

-(180 cm × 35kg) + (x cm × 63 kg) -(0 cm × 28 kg) ＝ ０

という式が成り立ちます。これを解いて、x ＝ 100 ㎝ が導かれます。このように、この人の、直立立位時の重心は床（足底）から１００㎝の高さにあることがわかります。

変わる身体重心位置

この直前の文章で、つり合いで求めた重心は、この人の、直立立位時の重心だと、太文字でことわりを入れておりました。人は関節で体節の位置を変えられます。重心は形で決まるという話をしましたが、逆に言えば、形が変われば重心位置も変わります。人の重心はいつも同じ位置にあるとは限らないのです。身体の外に出ることもあります。

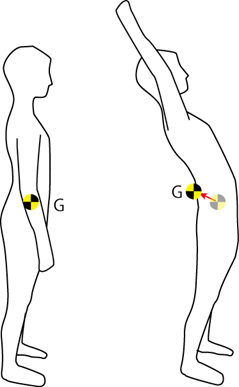
体節の重心

この授業の冒頭で、人の身体をロボットのように見立てる、という話をしました。今、身体をロボットのように関節で切り分け、上腕、前腕といった部品で成り立つと仮定します。身体を節で分ける、という意味で各部品を体節と呼びます。さて、体節は曲げたりできず、変形しないものと見立てることができます。実際には、人体はやわらかいので、変形しない、と見立てるのは多少無理があるのですが、仮に変形しないと考えれば、形が決まるので、三角形の重心のように、いつも変わらない一つの点に重心を定義できます。これは、人の運動を考える上で大変便利な考えです。これを剛体モデルと呼びます。剛体は「変形しない理想の物体」のことです。

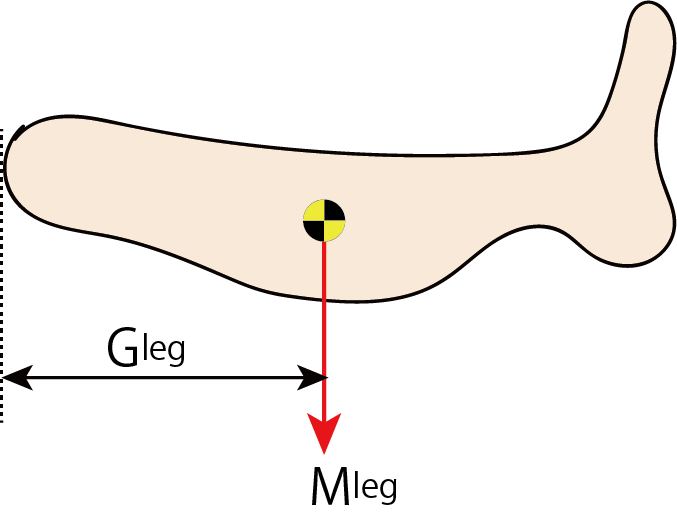
大腿や前腕を剛体と考えれば、重心は決まる。人によって体節の長さや重さは異なるが、体節長や体重比を使えば、どんな対象者でも剛体モデルで運動を考えることができる。そこで、昔の研究者は、屍体標本を使って体節の物性値を決める研究を行いました。今は違う方法でも物性値が求められるようになりましたが、私たちが運動をモデル化して考える上では、以前からある物性値を使っても大きな問題はありません。ここに、データを表でまとめておきます。

体節	定義	質量 （体重％）	重心（近位から％）
頭部（頸部含）	C7から頭頂まで	8	46.6
体幹	大転子から肩関節	49.7	0.5
上腕	肩関節から肘関節	2.8	43.6
前腕と手	肘関節から尺骨茎状突起	2.2	68.2
大腿	大転子から膝関節	10	43.3
下腿と足部	膝関節から内果	6.1	60.6
上肢	肩関節から尺骨茎状突起	5	53
頭と体幹と両上肢	大転子から肩関節	67.8	62.6
下肢	大転子から内果	16.1	44.7

計算で求める身体重心

冒頭で固くて長い板の下に体重計を置き、つり合い点を見つけることで重心を求める方法を紹介しました。今度はもう一つ別の方法、各体節の重心を合成して身体重心を求めてみます。

図のH、R、T、L、Fはそれぞれ、頭部、体幹（両上肢を含む）、大腿（左右）、下腿（左右）、足部（左右）の重心位置を示しています。それぞれの重さは、頭部10kg、体幹40kg、大腿10kg、下腿８kg、足部２kgだとします。足の重心位置を基準とし、そこから各重心までの距離は次のようになっているとします。

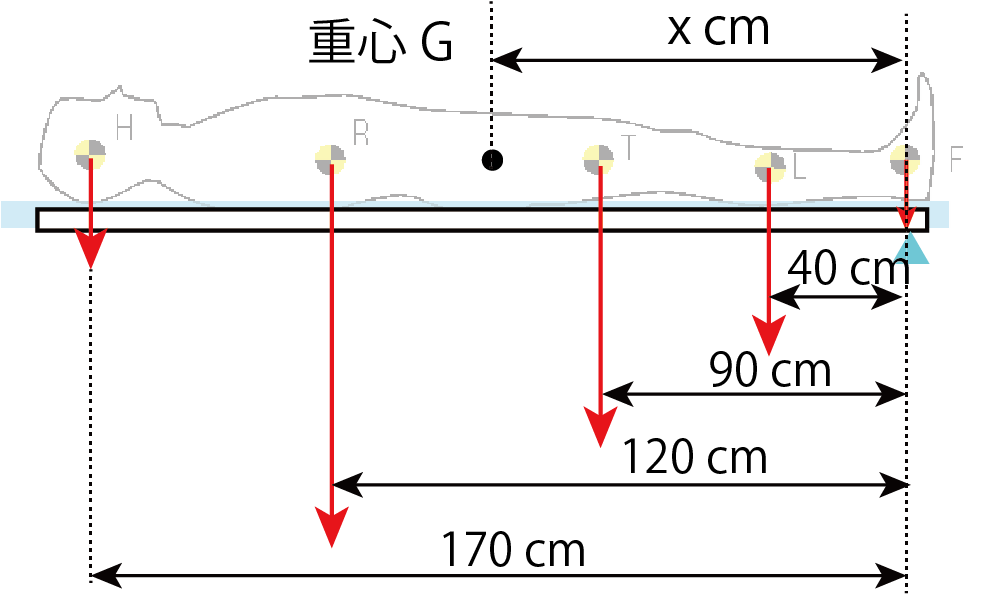
足の重心の位置を基準にしたので、そこを支点と考えると、体節の重心によって支点まわりには、反時計方向に、

10kg × 170cm + 40kg × 120cm + 10kg × 90cm + 8kg × 40cm + 2kg × 0cm 

のモーメントが生じていて、これと重心によるモーメント（ｘ × 体重）が等しくなる。
体重は（10kg + 40kg + 10kg + 8kg + 2kg）なので、70kgである。よって、重心までの距離ｘは
110cmとなる。このように、体節の重心から計算で重心位置を求められる。

「身体重心」のまとめ

• 身体重心もベッドを支える力などを頼りに釣り合い式で求められる。
• 関節で体節が動くことで、身体重心位置は変化する
• 動きがない剛体と、、体節の重心は身長比で位置、体重比で質量が求められる。

先頭に戻る