重心

重心とは

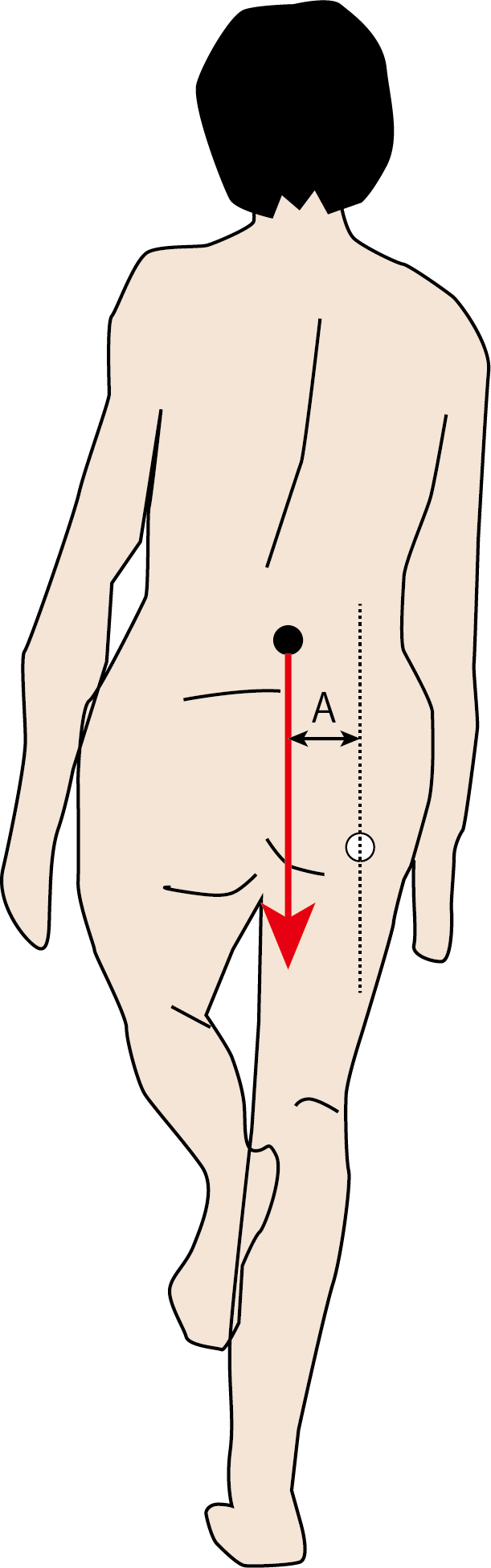
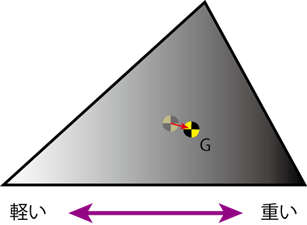
重心とは何か、というところから考えていきます。この図では片足で立っている人の重心を黒のマル印で示しています。この重心って、どのようにして「ここだ」とわかるのか、重心っていったい何なのか、ということを話していきます。

三角形の重心

三角形の重心を求めること、小学校か中学校くらいで取り組みませんでしたか？

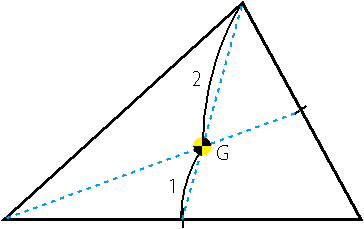
図のように、三角形の重心は頂点から対辺を二等分する点に線を引き、それが交わった点であるとか、対辺に引いた線を2対1に内分するなど、が思い出されます。こうして求めた重心って、一体何だったのか、それを一言でいえば、つり合いが取れる点だということです。

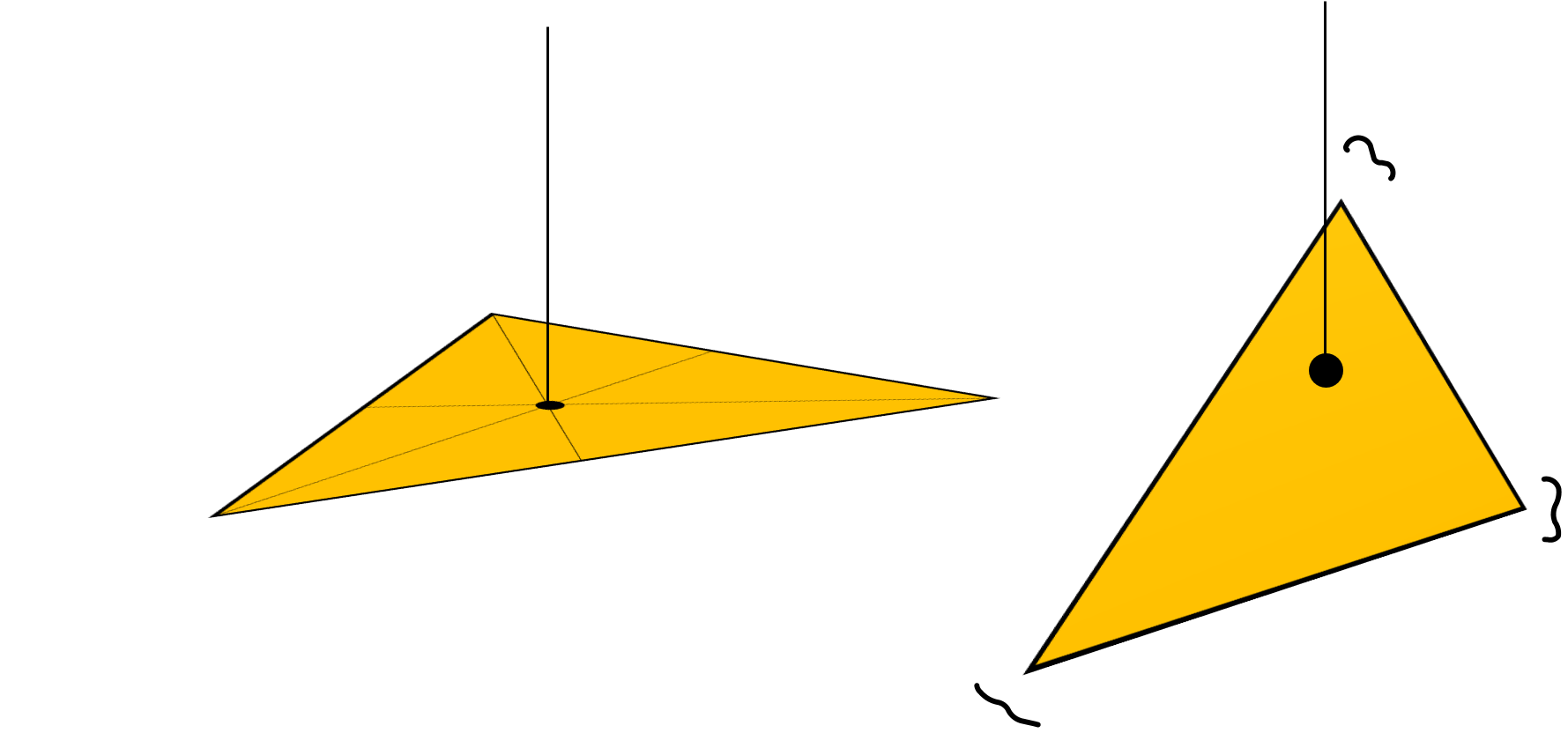
図は三角形のどこか一点にひもと取り付け、吊り下げている様子をしまします。左は重心、右は重心以外に取り付けたイメージです。重心を引っ張れば、ちょうどつり合いが取れるので平衡を保てます。一方、重心以外だと、三角形は傾いて吊り下げられます。

つまり、重心はその物体の持つ「つり合い点」と言えます。

車いすの重心

では、三角形ではなく、他の形、物体ではどうでしょうか。ここでは、臨床上も意味のある、車いすの重心を考えてみます。

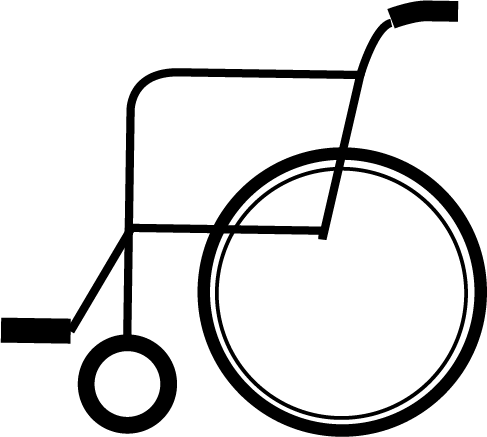
車いすは車輪があり、背もたれがあり、三角形と比べはるかに複雑な形をしています。でも、重心は「つり合い点である」ことを忘れなければ、簡単に求めることができます。三角形をつるしたように、ここでは車いすをつるして重心を求めてみます。

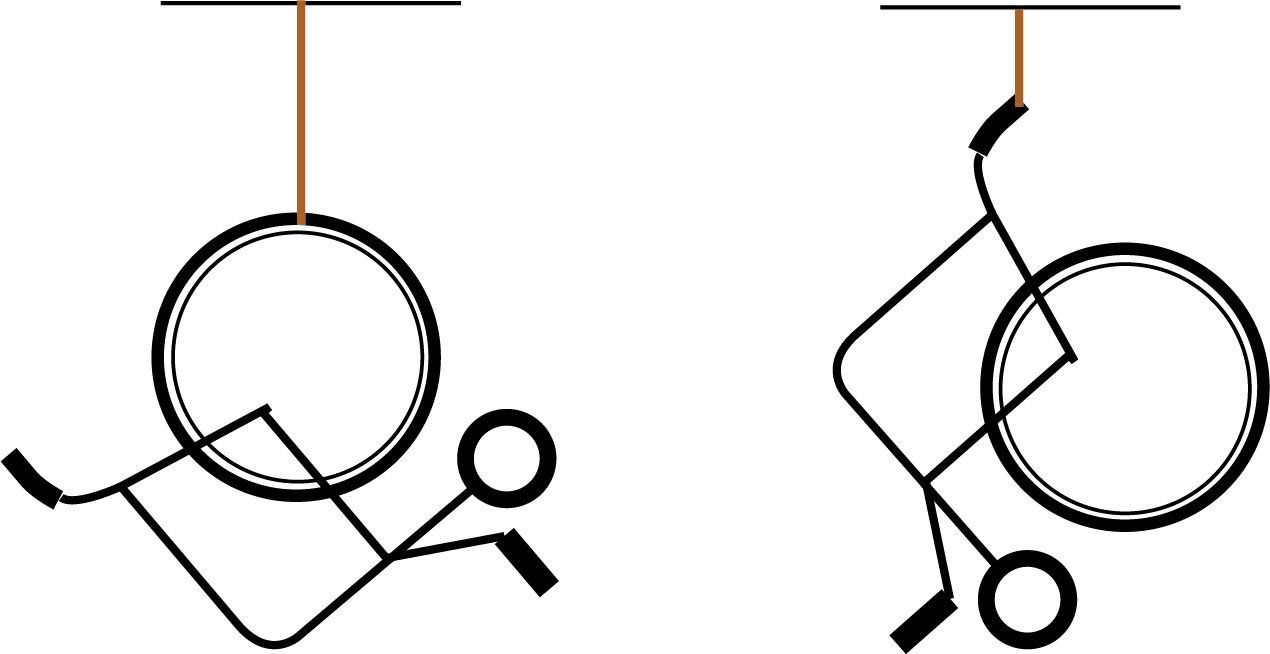
どこでもよいので、2か所にひもをつけ、それを天井にかけて車いすをつるすことをイメージしてください。つるした最初は揺れるかもしれませんが、そのうち静止します。その静止した状態がつり合いが取れいている状態です。支えから鉛直に下した腺が重心線です。

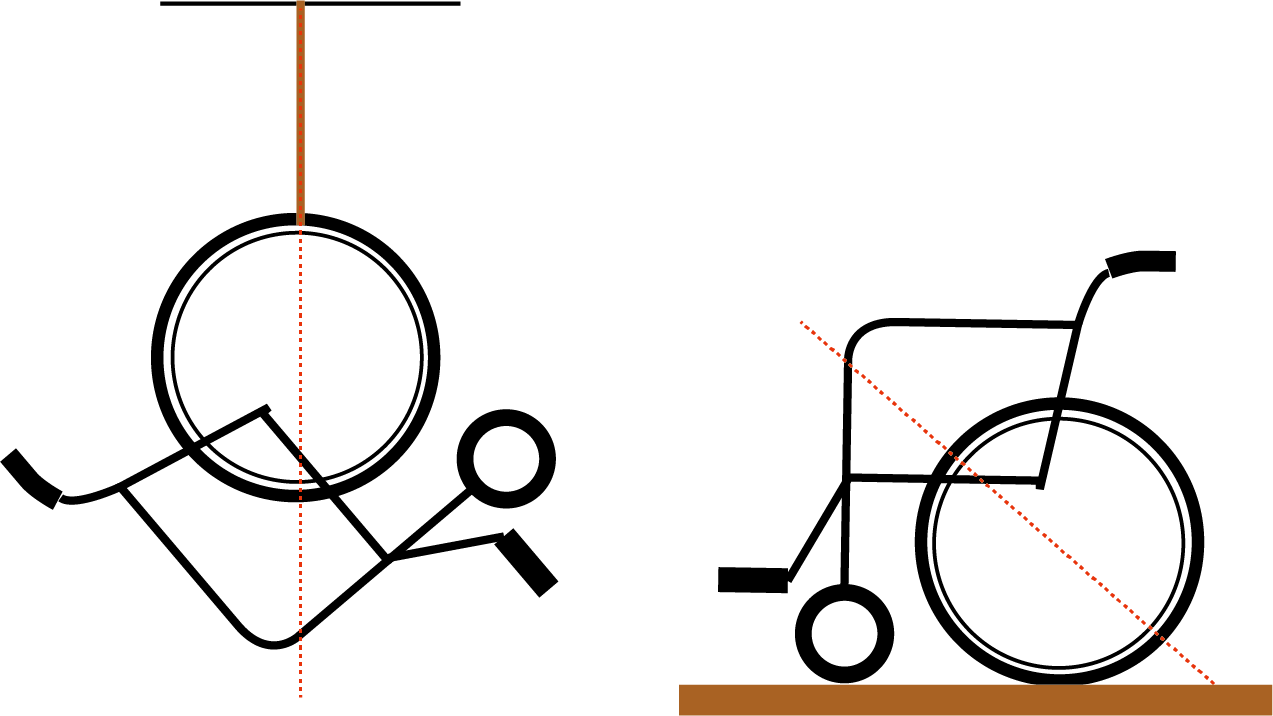
この重心線を控えておきます。重心はこの線上にあります。もう一方で吊り下げたときの重心線も控え、両者の交点を求めれば、それが重心点です。

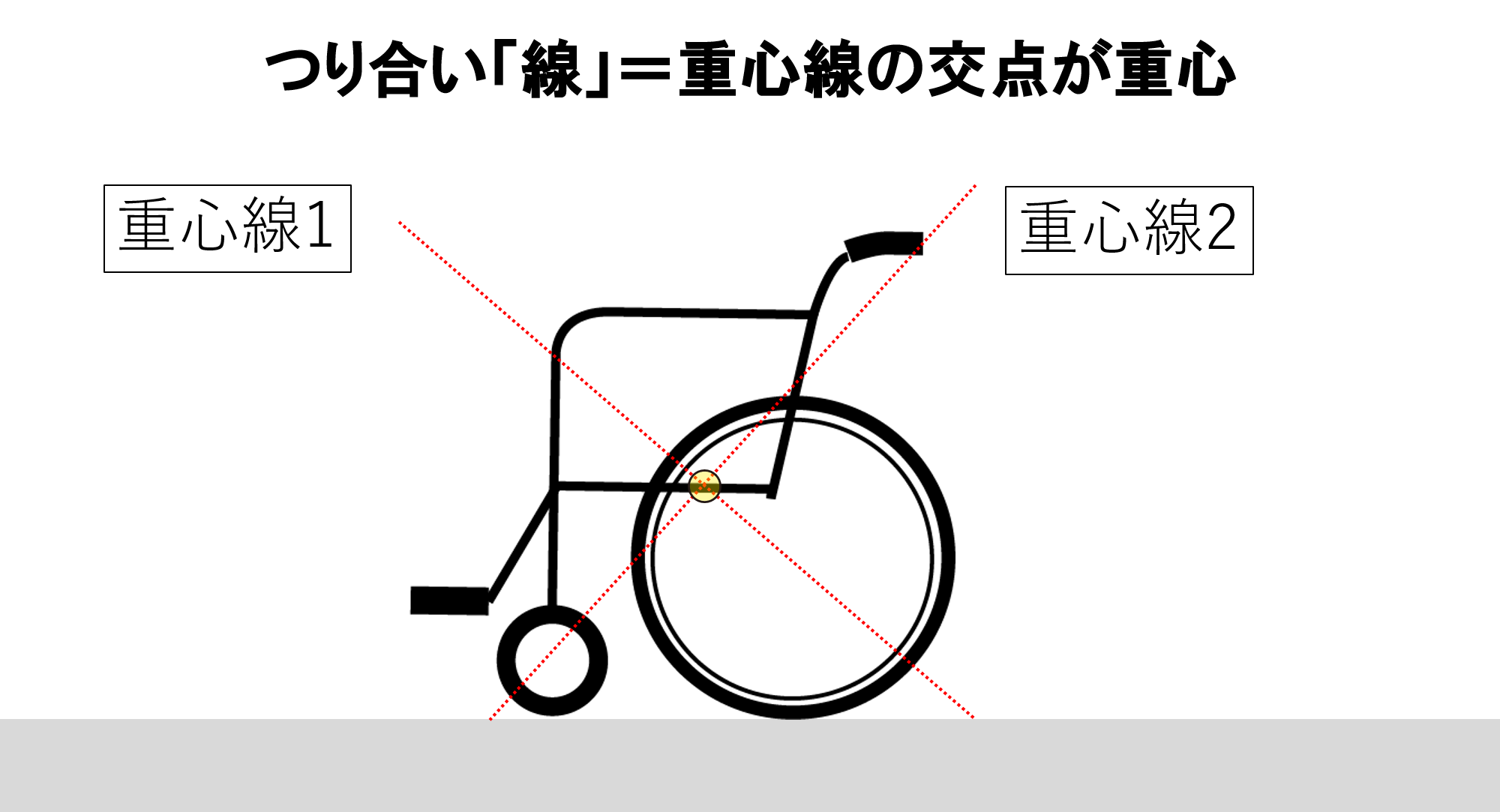
車いすに限らず、物体の重心は目に見えませんし、触ることもできません。力学上の概念です。重心は物体のつり合い点であるため、その物体の重りがまるで重心に集中しているような考えることができます。

重心の定義式

三角形の重心は「頂点とその対辺の中点へ引いた線を２：１に分割する点」のように求めることができました。三角形以外ではどうでしょうか？これは、定義が数式で次のようにまとめられます。

∫[(ρi×si)×Xi]dx=M×Gx

ここで、ρは密度、sは面積、ｘは位置、Mは全体の質量、GxがX方向の重心位置を表します。ここで、伝えたいのは、重心は形と密度で計算できる、ということです。もっと踏み込んでいうと、重心は形と密度（質量分布）で決まるということ。三角形の重心が先のように定義できましたが、三角形でも、密度分布が異なれば、重心は「頂点とその対辺の中点へ引いた線を２：１に分割する点」ではなく、別の点になります。

「重心」のまとめ

• 重心はつり合い点
• 形が決まれば重心も決まる
• 同じ形でも、質量分布（密度）が異なれば重心位置も変わる。

先頭に戻る